© Eberhard Haug 2003-2026
Optimale Darstellung dieser Website
bei aktiviertem
"Active Scripting"
(LED-Menü-Buttons)
In dieser Grundlagenrubrik geht es um den Vergleich von Strom- und Spannungsquellen, wobei uns beim Thema LED-Treiber natürlich bevorzugt die Stromquellen interessieren, die dann überwiegend konstanten Gleichstrom liefern.
Als komplexe Beispiele einer Wechselstromquelle werden verschiedene Fahrraddynamos genauer untersucht.
Der kurze Weg geht hier entlang:
Beispielhafte Betrachtung am Fahrraddynamo (24.7.2015)
Simulationen (24.7.2015)
Denksportaufgabe (24.7.2015)
Messwerte für den Nabendynamo Shimano DH-3N80 (23.9.2015)
Eine beispielhafte Betrachtung am Fahrraddynamo (24.7.2015)
Es wird immer wieder heftig diskutiert, ob ein Fahrraddynamo denn eine (Wechsel-) Spannungsquelle oder eine (Wechsel-) Stromquelle sei.
Nach genauerem Hinschauen stellt man fest, dass es eigentlich nur eine Frage der Betrachtungsweise und der Definition ist, aber eine Unterscheidung zwischen Strom- und Spannungsquelle dennoch Sinn macht.
Ersatzschaltbilder realer Quellen - die reale Stromquelle
Das Ersatzschaltbild einer realen Stromquelle besteht aus einer idealen Stromquelle mit dem konstanten Kurzschlussstrom I_k und einem parallelgeschalteten Innenwiderstand R_i (teilweise auch mit dem Leitwert G_i = 1 / R_i bezeichnet).
Die Leerlaufspannung der realen Stromquelle beträgt
U_l = I_k * R_i (1)
Die reale Spannungsquelle
Das Ersatzschaltbild einer realen Spannungsquelle besteht aus einer idealen Spannungsquelle mit der konstanten Leerlaufspannung U_l und einem in Serie geschalteten Innenwiderstand R_i.
Der Kurzschlussstrom[2] der realen Spannungsquelle beträgt
I_k = U_l/R_i (2)
Äquivalent
Aus den Gleichungen (1) und (2) ist ersichtlich, dass sich eine reale Stromquelle immer in eine elektrisch äquivalente reale Spannungsquelle umwandeln lässt, die dann beide denselben Innenwiderstand R_i haben:
R_i = U_l/I_k (3)
Strom- oder Spannungsquelle?
Ob man im Einzelfall nun von einer Stromquelle oder einer Spannungsquelle spricht, ist bei Angabe obiger Parameter also eigentlich gleichgültig, es sei denn, man schließt an beiden realen Quellen eine Last an.
Dann macht es durchaus Sinn, den Unterschied zwischen beiden Quellen z.B. anhand des Verhältnisses zwischen Innenwiderstand R_i (der bei äquivalenten Strom- und Spannungsquellen identisch ist) und einem angeschlossenen Lastwiderstand R_last wie folgt zu definieren:
Falls beide Widerstände gleich sind, hat man die Wahl.
Bei dieser Überlegung spielt es keine Rolle, ob man Gleich- oder (sinusförmige) Wechselgrößen nimmt. Statt ohmschen Widerständen werden dann Scheinwiderstände verwendet.
Beispiel Fahrraddynamo
Beim typischen 6V/3W-Fahrraddynamo beträgt der Lastwiderstand durch die beiden Glühbirnen R_last = 12 Ohm.
Für eine Aussage, ob Stromquelle oder Spannungsquelle gemäß obiger Entscheidungstabelle, müsste man - bei einem bestimmten Lastwiderstand R_last - also auch noch den Innenwiderstand R_i des Dynamos wissen.
Allerdings wird es beim Dynamo etwas schwieriger mit der Angabe von Innenwiderstand, Leerlaufspannung und Kurzschlussstrom, denn die praktische Erfahrung lehrt, dass zumindest die Leerlaufspannung stark von der Fahrgeschwindigkeit bzw. Dynamodrehzahl abhängig ist.
Lediglich der ohmsche Widerstand R_o der Dynamowicklung lässt sich sehr einfach mit einem Ohmmeter messen.
Messungen an einem Fahrraddynamo
Bei einem Seitenläufer AXA HR Traction beträgt R_o ziemlich genau 2Ω. Dieser Wert ist aber sicher nicht der gesuchte Innenwiderstand R_i des Dynamos und hilft deshalb zunächst nicht viel weiter.
Der Kurzschlussstrom eines Dynamos ist zwar ebenfalls einfach zu messen, ist jedoch drehzahlabhängig (wenn auch deutlich weniger als die Leerlaufspannung).
Einige Kurzschlussstromwerte wurden an einem (gebrauchten) AXA HR Traction zusammen mit der Frequenz[1] wie folgt gemessen:
Da die Leerlaufspannung bei älteren Dynamos (so auch beim betrachteten AXA HR Traction) meist mittels Z-Dioden spannungsbegrenzt ist, kann über die Leerlaufspannung des Dynamos nur dann eine Aussage gemacht werden, wenn man die Spannungsbegrenzung entfernt.
Bei einem "kastrierten" AXA HR Traction (demselben Exemplar wie oben) sind einige Messwerte für die Leerlaufspannung wie folgt:
Die Leerlaufspannung des Dynamos kann bei höheren Fahrgeschwindigkeiten ohne Spannungsbegrenzung generell stolze Werte annehmen (bei manchen anderen Dynamos teilweise sehr viel mehr als beim AXA HR), die - wie man als Radler mit einem alten Dynamo-Glühbirnchenlicht weiß - ein Rücklicht ohne Vorderlicht ggf. schnell dauerhaft erlöschen lässt.
Der gesuchte dynamische Innenwiderstand lässt sich gemäß oben definierter Beziehung R_i = U_l/I_k nach Gleichung (3) schließlich aus den Messwerten in Abhängigkeit von der Fahrgeschwindigkeit (deshalb dynamisch) bestimmen.
Einen wesentlichen Anteil am dynamischen Innenwiderstand des Dynamos hat sicherlich die Wicklung des Dynamos, die vereinfacht eine Spule mit einer bestimmten Induktivität L darstellt.
Deren induktiven Widerstand ωL (= 2πf * L) kann man sich bei einem vereinfachten Dynamo-Ersatzschaltbild in Serie mit dem bereits ausgemessenen ohmschen Widerstand R_o denken, d.h. für den Scheinwiderstand des Dynamos gilt:
(R_i)² = (ωL)² + (R_o)² (4)
und zwar unabhängig davon, ob man den Dynamo als Stromquelle oder als (unbegrenzte) Spannungsquelle betrachtet.
Messungen ausgewertet
Aus obigen Messwerten und Gleichung (4) berechnen sich der von der Frequenz abhängige dynamische Innenwiderstand R_i und die Induktivität L der Dynamowicklung für mein Testexemplar aus den Messwerten wie folgt:
Falls keine Spannungsbegrenzung am Dynamo vorliegt (wie bei diesen Messungen), sind die Ströme und Spannungen (mehr oder weniger) sinusförmig und die Angaben sind demnach Effektivwerte.
Die aus der Frequenz[1] der Ströme und Spannungen berechnete Fahrgeschwindigkeit ist jeweils für ein 28"-Rad angegeben (einschließlich 6% Seitenläuferkorrektur für den verwendeten Felgendynamo).
Fazit für den AXA HR Traction
Der Kurzschlussstrom des untersuchten Dynamos ist bei flotter Fahrgeschwindigkeit ab ca. 20 km/h nahezu unverändert und nur wenig größer als bei ca. 5 km/h (Schrittgeschwindigkeit).
Die Leerlaufspannung und damit der dynamische Innenwiderstand des Dynamos R_i nehmen dagegen stetig und stark mit der Geschwindigkeit zu.
Man kann bei dem untersuchten Fahrraddynamo also durchaus von einer (Wechsel-) Stromquelle statt von einer (Wechsel-) Spannungsquelle sprechen, was auch obige Unterscheidungsdefinition zwischen beiden bestätigt, denn der dynamische Innenwiderstand ist bei diesem Dynamo im interessanten Geschwindigkeitsbereich mit bis zu über 30Ω um einiges größer als der Nennlastwiderstand von 12Ω.
Lediglich bei sehr geringen Fahrgeschwindigkeiten ist der dynamische Innenwiderstand dieses Dynamos mit unter 10Ω geringfügig kleiner als der Lastwiderstand in Form zweier Glühlampen (der bei Unterspannung auch etwas kleiner als 12Ω ist).
Die berechnete Induktivität L für das Ersatzschaltbild nimmt beim betrachteten Dynamo nur geringfügig mit höherer Geschwindigkeit ab, d.h. bis zur untersuchten Geschwindigkeit ist keine magnetische Sättigung der Dynamospule festzustellen (wie oft behauptet wird), es ist lediglich die mit zunehmendem Strom und zunehmender Frequenz abnehmende Induktivität, was für jede Spule mit Kern gilt.
Falls man das Ersatzschaltbild für den Dynamo etwas komplexer gestaltet und einen weiteren Widerstand für die Eisenverluste einführt, ergibt sich bei geschickter Wahl der Bauteilewerte ein von der Geschwindigkeit nahezu unabhängiger Induktivitätswert.
Bei Gelegenheit werde ich noch die elektrischen Werte eines Nabendynamos im echten Fahrbetrieb aufnehmen.
Messwerte für den Nabendynamo DH-3N80 (23.9.2015)
Beim Seitenläufer war der Aufwand für die Messungen von Kurzschlussstrom und Leerlaufspannung mit einer Standbohrmaschine relativ gering. Diese einfache Methode klappt mit einem Nabendynamo allerdings nur bedingt, denn dieser sollte zum Messen mit höheren Geschwindigkeiten eingespeicht sein.
Im Schweiße meines Angesichts
Da für meine Messungen am DH-3N80 ein aufwendiger Prüfstand nicht zur Diskussion stand, habe ich mir eine völlig andere Methode ausgedacht, wozu ich mich einfach auf mein Trekking-Rad gesetzt und die Dynamo-Messwerte "erfahren" und aufgezeichnet habe - nämlich mit einem Logging-DMM BM525 im Rucksack.
Da ich bis zu 50km/h aufzeichnen wollte, habe ich mir eine kurze steile Strecke ausgesucht, die ich dann aber wegen den beiden verschiedenen Messungen gleich zweimal wieder hochfahren musste ...
Kurzschluss
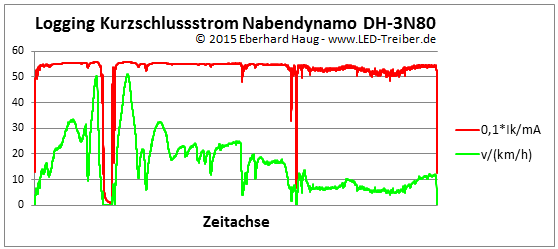
Zuerst habe ich den Kurzschlussstrom gemeinsam mit der Fahrgeschwindigkeit (genau genommen der Frequenz des Kurzschlussstromes) aufgezeichnet - eine in diesem Zusammenhang sehr hilfreiche Eigenschaft des BM525:
Um zusammenpassende Vertikalmaßstäbe zu bekommen, ist im Diagramm 1/10 des Kurzschlussstromes dargestellt.
Leider habe ich bei meiner ersten Abfahrt eine Baustelle nicht bedacht, die mich per Verkehrsampel zum Anhalten zwang (siehe erster Einbruch mit kurzer Pause im Diagramm).
Meine "Kurzschlussfahrt" mit über 50 Sachen habe ich vor dem schweißtreibenden Wiederaufstieg noch mit einem Trip durch die Stadt verlängert (der ungleichmäßige Geschwindigkeitsverlauf bis zum zweiten kurzen Stop).
Am Verlauf des Kurzschlussstromes sieht man, dass bereits ab 10km/h mehr als 500mA erreicht werden, die bis 50km/h nur noch sehr wenig ansteigen - ein ziemlich solider Konstantstrom!
Leerlauf
Nach einer kurzen Verschnaufpause und dem Umstecken der Messstrippen auf Spannungsmessung ging meine zweite Abfahrt diesmal ohne Stop an der Ampel vorbei:
Lediglich eine unübersichtliche Kurve hat mich kurz ausgebremst, um dann doch noch über 50km/h zu kommen.
Unten angekommen, habe ich direkt umgedreht und bin denselben Weg wieder hochgestrampelt - deutlich langsamer, wie man sieht ...
Bei diesem Diagramm sticht sofort ins Auge, dass die Leerlaufspannung sehr genau linear von der Geschwindigkeit abhängt (nahezu deckungsgleiche Kurvenverläufe): Jeder zusätzliche km/h erzeugt eine um ca. 1 Volt höhere Leerlaufspannung.
Dieser Zusammenhang wird nach der Auswertung in einem weiteren Diagramm direkt in Abhängigkeit von der Fahrgeschwindigkeit deutlich.
Die Messwerte auf einen Nenner gebracht
Diese beiden zeitabhängigen Aufzeichnungen zeigen zwar sehr schön meinen tatsächlichen Fahrverlauf[5], sind aber in dieser Form noch nicht besonders hilfreich, nämlich um die gesuchten geschwindigkeitsabhängigen Zusammenhänge besser erkennen zu können.
Um diese Zusammenhänge zu erhalten, habe ich die aufgezeichneten zeitabhängigen Messwerte zunächst per Tabelle nach Frequenz bzw. daraus berechneter Geschwindigkeit sortiert, mir daraus geeignete Messwertpaare für bestimmte Geschwindigkeiten herausgesucht (die Auswahl ist aufgrund der sehr vielen erfassten Messwerte[6] groß) und in einer neuen Tabelle zusammengefasst, in der (wie beim AXA HR) der dynamische Innenwiderstand und daraus die Induktivität der Dynamowicklung berechnet wurde:
Die blau unterlegten Werte sind von besonderem Interesse.
Diagramm in Abhängigkeit von der Geschwindigkeit
Und schließlich noch Leerlaufspannung und Kurzschlussstrom des DH-3N80 nach der "Zeit-Geschwindigkeits-Transformation" als übersichtliches Diagramm dargestellt:
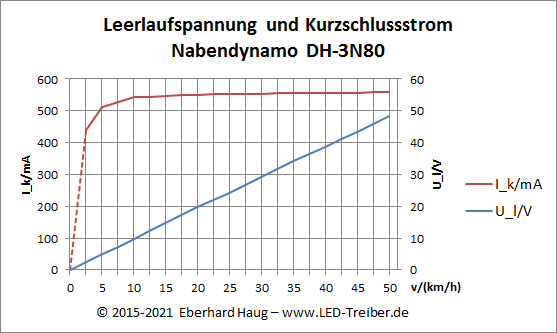
In diesem Diagramm entspricht der Kurzschlussstrom bis 2,5km/h nicht wirklich dem tatsächlichen Verlauf und ist deshalb als gestrichelte Ursprungsgerade dargestellt (für einen genaueren Verlauf an dieser Stelle wären Messwerte für <2,5km/h nötig gewesen).
Einige Parameter zum Berechnen
Falls jemand selbst solche Untersuchungen und Berechnungen anstellen möchte, hier noch der einfache Zusammenhang zwischen Frequenz und Fahrgeschwindigkeit beim Nabendynamo (hier für den Seitenläufer):
Fahrgeschwindigkeit (km/h) = Dynamofrequenz (Hz) * 3.600 * Radumfang (mm) / (Polpaarzahl * 10^6)
"Dynamofrequenz" ist die Frequenz des gemessenen Kurzschlussstromes bzw. der gemessenen Leerlaufspannung.
Bei meinem 28”-Rad beträgt der Radumfang 2.188 mm und die Polpaarzahl des DH-3N80 ist bei der 36-Speichenausführung 14 (28 Pole).
Der Faktor 10^6 im Nenner ergibt sich aus der Umrechnung von mm in km.
Mein Tacho hat bei meinen beiden Messfahrten übrigens genau die berechnete Maximalgeschwindigkeit angezeigt (keine Überraschung, denn im Tacho-Setup ist ein Radumfang von 2.188 mm angegeben).
Fazit für den Shimano DH-3N80
Beim DH-3N80 ändert sich der Kurzschlussstrom zwischen 5km/h und 50km/h um <10%.
Das ist eine sehr schöne Konstant(wechsel)stromquelle - noch etwas besser als beim AXA HR, auch wenn der Kurzschlussstrom nicht so hoch ist (dafür die Leerlaufspannung bzw. der dynamische Innenwiderstand).
Im Unterschied zum AXA HR ist die berechnete Induktivität der Dynamo-Wicklung bereits ab 5km/h so gut wie konstant, nämlich im Mittel 156mH.
Das liegt daran, dass dieser Nabendynamo zumindest bis 50km/h sehr geringe Eisenverluste hat. Allerdings ist der Wicklungswiderstand mit gemessenen 4,1Ω etwa doppelt so groß und die Frequenz von Strom bzw. Spannung ist bei gleicher Fahrgeschwindigkeit deutlich kleiner als beim Seitenläufer.
Der große Vorteil beim DH-3N80 ist, dass man bei Simulationen statt dem frequenzabhängigen Widerstand Ri (laut Tabelle) einfach mit einer Spule mit konstanter Induktivität arbeiten kann.
Ersatzschaltbilder für den DH-3N80
Das naheliegende, sehr einfache Ersatzschaltbild des DH-3N80 ist neben einer Sinuskonstantstromquelle parallel geschaltet eine Spule mit 156mH Induktivität und einem in Serie zur Spule geschalteten ohmschen Widerstand von 4,1Ω:
Da die Amplitude von I_k so gut wie konstant ist, muss man beim geschwindigkeitsabhängigen Simulieren mit diesem Ersatzschaltbild nur die Frequenz des Sinusstromes berücksichtigen.
Wie oben diskutiert, gibt es auch das elektrisch äquivalente Ersatzschaltbild mit einer Sinusspannungsquelle in Serie mit derselben LR-Serienschaltung (also 156mH und 4,1Ω).
Da aber die dabei verwendete Leerlaufspannung U_l abhängig von der Frequenz (bzw. Fahrgeschwindigkeit) ist, wird die Simulation damit umständlicher, sollte aber an derselben Last dennoch auch dasselbe Ergebnis liefern wie mit der Stromquelle.
Erst bei genauerem Hinschauen wird man die Unterschiede beim Simulieren mit den beiden ziemlich einfachen Ersatzschaltbildern feststellen. Für noch bessere Ergebnisse müsste man komplexere Ersatzschaltbilder entwerfen. Es wird den Aufwand aber kaum wert sein.
Dynamoverluste
Interessant wird die Unterscheidung zwischen Ersatzstromquelle und Ersatzspannungsquelle im Leerlauf- und Kurzschlussfall, falls man damit die Verluste im Dynamo selbst bestimmen möchte.
Nun, beide Ersatzschaltbilder liefern zunächst nur an einer äußeren Last an den beiden Anschlüssen mit den in der Tabelle aufgeführten Werte für Kurzschlussstrom bzw. Leerlaufspannung in etwa dasselbe elektrische Verhalten und dürfen nicht zum Simulieren des Dynamos selbst verwendet werden.
Hilfreich bei Simulationen (24.7.2015)
Mit den in obiger Tabelle für den AXA HR zusammengestellten Werten für Frequenz (mit korrespondierender Fahrgeschwindigkeit), Kurzschlussstrom (falls Stromquelle) oder Leerlaufspannung (falls Spannungsquelle) und deren dynamischem Innenwiderstand R_i (dargestellt als Spule L in Serie zu deren konstantem ohmschen Widerstand R_o), kann man durchaus per Dynamo versorgte elektronische Schaltungen sehr gut auf deren Funktionstüchtigkeit und Verhalten simulieren, sofern der Blindanteil der Last verhältnismäßig klein ist.
Zum Beispiel mit der als Dynamo-LED-Treiber vorgeschlagenen Spannungsverdoppler- bzw. "Stromhalbierer"-Schaltung und einer K2-LED als Last liefert die Simulation mit den obigen AXA-HR-Specs bei 40km/h ca. 336mA LED-Strom.
Bei nur 20km/h simuliert, ergeben sich ca. 331mA LED-Strom, also nur knapp weniger, so dass man bei diesem Dynamo wirklich von einer guten Stromquelle sprechen kann.
Simuliert man dieselbe Schaltung statt mit einer Stromquelle mit der äquivalenten Spannungsquelle, beträgt der Unterschied beim LED-Strom nur wenige mA, wodurch die äquivalente Betrachtungsweise nochmals bestätigt wird.
Dieser simulierte LED-Strom wird schließlich auch noch durch Messungen an einer realisierten Schaltung bestätigt[3].
Simulationsergebnisse für den DH-3N80 (24.9.2015)
Im Leerlauf
Zunächst wurde mittels Simulation des gefundenen nahe liegenden Ersatzschaltbilds des DH-3N80 (nämlich mit der Ersatzstromquelle) bestätigt, dass ein Frequenz-Sweep von 0 bis 88,87Hz mit I_k = 558mA auch tatsächlich das obige Diagramm für die Leerlaufspannung liefert:
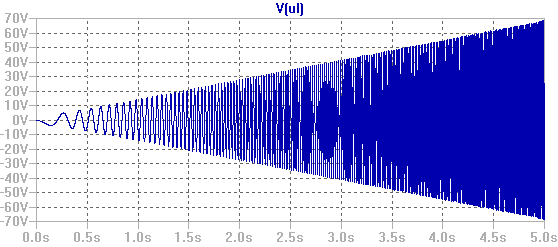
Die Zeit/Frequenz-Parameter wurden hier so gewählt, dass 5 sec auf der Zeitachse genau 50km/h[7] entsprechen, so dass man aus dem Diagramm direkt die Amplitude der Leerlaufspannung für eine bestimmte Fahrgeschwindigkeit ablesen kann (dabei unten stehende Tipps 1 und 2 beachten).
Dynamo-LED-Treiber simuliert (24.9.2015)
Der DH-3N80 kann laut Simulation mit obigem Ersatzschaltbild z.B. acht in Serie geschaltete K2-LEDs bei 50km/h mit nahezu 6 Watt per Spannungsverdoppler-Schaltung versorgen. Der LED-Strom ist dabei ca. 235mA.
Per Brückengleichrichter-Schaltung kann man vier in Serie geschaltete K2-LEDs bei 50km/h laut Simulation sogar mit knapp über 6 Watt befeuern. Der LED-Strom ist dabei ca. 460mA.
Diese simulierten Werte habe ich bislang aber noch nicht praktisch überprüft.
Praktische Tipps (24.7.2015)
Tipp 1:
Bei der Simulation beachten, dass die Effektivwerte aus obiger Tabelle (sowohl Ströme als auch Spannungen) normalerweise in Spitzenwerte umgerechnet werden müssen.
Tipp 2:
Umgekehrt Simulationsergebnisse wieder von Spitzenwerten in Effektivwerte umrechnen bzw. die Effektivwerte der Ergebnisse vom Simulationsprogramm anzeigen lassen.
Falls Ergebnisse um den Faktor √2 falsch sind, hat man mit großer Wahrscheinlichkeit an irgend einer Stelle die Tipps 1 und 2 nicht beachtet.
Tipp 3:
Bei Schaltungen mit Gleichrichtung (das dürfte bei Dynamo-LED-Treibern der Normalfall sein) beachten, dass der Spitzenwert der Spannung erzeugt wird (maximal der Spitzenwert der Leerlaufspannung), den die nachgeschaltete Schaltung auch vertragen muss.
Falls die gleichgerichtete Spannung nicht durch die versorgten LEDs begrenzt wird (der Normalfall), muss man die gleichgerichtete Spannung z.B. mit einer Z-Diode begrenzen. Die Z-Spannung wird geringfügig größer als die erwartete Nennbetriebsspannung gewählt.
Die Z-Diode muss dann in der Lage sein, den bei Erreichen der Z-Spannung fließenden Strom zu verarbeiten, sprich die erzeugte Wärme abzuführen.
Am Besten, man simuliert die Gleichrichtung mit vorhandener Z-Diode, aber ohne die weitere Last und bestimmt die dann in der Z-Diode erzeugte elektrische Leistung.
Wie kann man feststellen, ob in einer kleinen geschlossenen Metallbox mit zwei isolierten Anschlussbuchsen entweder eine
Gleichstromquelle mit I_k = 1A und Ri = 10Ω
oder eine
äquivalente Gleichspannungsquelle mit U_l = 10V und Ri = 10Ω
untergebracht ist (Bezeichnungen s.o.)?
Es stehen beliebige Messgeräte[4], ohmsche Lastwiderstände[4] und beliebig Zeit zur Verfügung, die Box darf aber natürlich nicht geöffnet werden.
Viel Spaß beim Überlegen!
(Nach genauem Studieren obigen Beitrags sollte die Lösung einfach sein.)
[1] Die Frequenz wurde beim Messen (mittels Standbohrmaschine) natürlich so eingestellt, dass sich die gewünschte Fahrgeschwindigkeit ergibt.
[2] Den Kurzschlussstrom darf man für längere Zeit nur bei Dynamos und Generatoren messen, deren Maximalstrom man ungefähr kennt.
Bei Akkus und Batterien ist (z.B. zur Bestimmung des Innenwiderstandes) eine Messung des Kurzschlussstromes bereits grenzwertig und sollte nur für sehr kurze Zeit erfolgen, wenn überhaupt. Es gibt auch noch etwas weniger massive Methoden als per Kurzschluss, um den Innenwiderstand zu bestimmen.
[3] Diese Messung wurde genau genommen mit einer älteren Luxeon-LED gemacht. Eine Simulation für die Luxeon-LED liefert jedoch nahezu denselben LED-Strom.
[4] So man dieselben überhaupt benötigt ...
[5] Ich ich erinnere mich noch genau, welcher Peak an welchem Ort ist.
[6] Alle 50msec wurde ein neuer Messwert erfasst und aufgezeichnet.
[7] Nach 5 sec beträgt die Frequenz des sinusförmigen Stromes 88,87Hz.