© Eberhard Haug 2003-2025
Optimale Darstellung dieser Website
bei aktiviertem
"Active Scripting"
(LED-Menü-Buttons)
An dieser Stelle werden verschiedene Verfahren diskutiert, wie man die Fakultät großer Zahlen auf einem kleinen AVR-µC berechnen kann. Auch werden Laufzeiten von Programmen in C und s’AVR verglichen.
Der kurze Weg geht hier entlang:
Schnelle Faktorielle - große Fakultätsberechnungen mit einem ATmega1284 (10.6.2019)
Rekursive Berechnung in die Tat umgesetzt (1.1.2021)
Die klassische Methode (10.6.2019)
Softwaretricks, MOD_DIV10 (10.6.2019)
Programmspeicherbedarf (10.6.2019)
Berechnungen auf kleineren ATmegas mit serieller Ausgabe (30.12.2020)
Turbo-Fakultät per kombinierter Binär/Dezimal-Multiplikation (25.1.2021)
5000! mit Delphi (25.1.2021)
5000! mit dem ATmega1284 (17.2.2021)
Schnelle Faktorielle - große Fakultätsberechnungen mit einem ATmega1284
10.6.2019
Anhand der relativ einfachen, aber sehr stack- und rechenintensiven Ackermann-Funktion wurde bereits gezeigt, dass strukturiertes AVR-Assembler-Programmieren mit s'AVR nicht nur Spaß machen kann, sondern auch noch eine sehr gute Performanz ergibt.
Nun, rekursive Funktionen sind eher etwas für Mathematiker, Informatiker und Programmierer, denn man kann sich solche Funktionen (insbesondere wie im Falle Ackermann) nicht immer einfach vorstellen.
Deshalb soll nun ein weiteres, deutlich komplexeres Beispiel schließlich ohne Rekursion folgen, das zum Bestimmen sehr großer Fakultäten einen ATmega1284 als Rechenknecht einsetzt, der mit s’AVR besonders beeindruckt.
Die Fakultät (teilweise auch Faktorielle genannt, im Englischen Factorial) einer Zahl z ergibt sich aus der Multiplikation aller natürlichen Zahlen von 1 bis z, also 1 * 2 * 3 * ... * z, die mit steigendem z sehr schnell große Werte annimmt. Verkürzt schreibt man für dieses Produkt einfach "z!".
Je nach verfügbarem (Taschen-) Rechner kann man per Fakultät-Taste/Funktion folgende Falkultäten gerade noch ganzzahlig als Dezimalzahl (also ohne 10er-Exponent) berechnen und darstellen lassen:
11! = 39916800 (8 Digits),
12! = 479001600 (9 Digits),
13! = 6227020800 (10 Digits, Kc-S56, SR-50, TI-30, TI-83 und sehr viele mehr),
14! = 87178291200 (11 Digits, Excel, Google direkt im Suchfenster)
17! = 355687428096000 (15 Digits, wissenschaftlicher Galaxy-Rechner)
18! = 6402373705728000 (16 Digits, wissenschaftlicher iPhone-Rechner)
21! = 51090942171709440000 (20 Digits, DuckDuckGo-Suchmaschine) oder gar
29! = 8841761993739701954543616000000 (31 Digits, wissenschaftlicher Windows-Rechner)
Der wissenschaftliche Rechner namens SpeedCrunch (verfügbar für Windows, Linux und macOS) mit teilweise sehr ausgefallenen Funktionen und mit sehr vielen Stellen Genauigkeit zeigt per Gamma-Funktion Γ(z+1) = z! maximal Γ(58) = 57! mit 77 Stellen und 13 Endnullen ganzzahlig an.
Der Online-Rechner JavaScripter schreckt schließlich auch vor 12000! mit 43742 Stellen (und 2998 Endnullen) nicht zurück. Bei 12001! ist aber auch hier Schluss.
Die ganzzahlige Darstellung ist unter anderem dann hilfreich, wenn man wirklich alle Dezimalstellen sucht oder auch nur die Anzahl der Endnullen einer großen Fakultät bestimmen will - letzteres eine kleine Denksportaufgabe aus meiner Schulzeit (die man ggf. in kurzer Zeit sogar für 1000! leicht durch Kopfrechnen lösen kann).
Auch rekursiv
Nun soll nicht verschwiegen werden, dass man eine Fakultät auch rekursiv berechnen kann, nämlich anhand der Definition z! = z * (z-1)! mit 1! = 0! = 1, was man sich (im Unterschied zur Ackermann-Funktion) sogar sehr gut vorstellen kann.
Auch programmiertechnisch wird das sehr einfach, z. B. in Java oder C-Sprache wie folgt (man beachte, dass "fakul" sich selbst aufruft = rekursiv):
long fakul(long z)
{
if (z>1) return (z * fakul(z-1));
else return(1);
}
Es gibt davon viele Varianten und natürlich auch C-typische Verstümmelungen ...
Die Fakultät in Pascal/Delphi als rekursive Funktion formuliert, könnte so aussehen:
function fakul(z: int64): int64;
begin
if z = 1 then fakul := 1
else fakul := z * fakul(z-1);
end;
Zum rekursiven Berechnen einer Fakultät fängt man also mit dem höchsten Wert z an und multipliziert dann immer weiter mit der nächst kleineren Ganzzahl bis herunter zu 1.
Im Unterschied zur Ackermann-Funktion steigt die Rekursionstiefe stetig an, um dann bei Erreichen von z=1 rasch wieder stetig abgebaut zu werden.
Bei dieser rekursiven Methode wird man sehr schnell (nämlich für z>20) den zulässigen Wertebereich von "long" bzw. "int64" überschreiten. Das Maximum mit der rekursiven Methode wäre bei den genannten Programmbeispielen also 20! = 2432902008176640000. Das sind immerhin 19 Dezimalstellen (und 4 Endnullen).
Rekursive Berechnung in die Tat umgesetzt (1.1.2021)
Nun wollte ich es doch etwas genauer wissen und habe die rekursive Methode auf einem ATmega328P umgesetzt, nachdem ich eine serielle Schnittstelle für die Ausgabe hatte.
Damit wirklich kein Bit verschwendet wird, sollte die untersuchte Funktion wie folgt lauten:
unsigned long fakul(int z)
{
if (z>1) return (z * fakul(z-1));
else return(1);
}
Um die maximal mögliche Fakultät zu finden, habe ich einfach eine Schleife programmiert:
for (z = 1; z <= 22; z++)
{
LED_ON;
fakul(z);
LED_OFF;
printf("Fakultaet von %2d = %20lu\n", z, fakul(z));
_delay_ms(1); // short LOW pulse for the scope/LED
}
Die Ernüchterung kam aber schnell, denn bereits bei 12! war Schluss mit lustig:
Fakultaet von 1 = 1
Fakultaet von 2 = 2
Fakultaet von 3 = 6
Fakultaet von 4 = 24
Fakultaet von 5 = 120
Fakultaet von 6 = 720
Fakultaet von 7 = 5040
Fakultaet von 8 = 40320
Fakultaet von 9 = 362880
Fakultaet von 10 = 3628800
Fakultaet von 11 = 39916800
Fakultaet von 12 = 479001600
Fakultaet von 13 = 1932053504 (statt 6227020800)
Fakultaet von 14 = 1278945280 (statt 87178291200)
Ab 13! sind die Ergebnisse nicht mehr korrekt.
Die Berechnung von 12! dauert allerdings auch nur 54 µs @16 MHz.
Nun, das liegt daran, dass "long" nicht in jeder Programmiersprache 64 Bit sind, sondern bei GCC halt nur 32 Bits.
Doch mit "uint64_t" oder "unsigned long long" (statt "unsigned long") klappt schließlich die rekursive Berechnung auch bis 20!, also:
uint64_t fakul(int z)
{
if (z>1) return (z * fakul(z-1));
else return(1);
}
Aber jetzt bekomme ich das 64-bit-Ergebnis trotz korrekter Formatierung nicht mehr per printf als Dezimalzahl ausgedruckt - Frust in C!
Erst per umständlichem Aufteilen auf 2x 32 Bit im Hex-Format klappt das serielle Ausgeben schließlich korrekt bis maximal 20! (wie oben erwähnt):
LED_ON;
f=fakul(z);
LED_OFF;
f1 = (f >> 32);
f2= f & 0xffffffff;
printf("\nFakultet %2d = %08lX%08lX", z, f1, f2);
Und hier die HEX-Ausgabe auf dem Terminal:
Fakultaet 1 = 0000000000000001
Fakultaet 2 = 0000000000000002
Fakultaet 3 = 0000000000000006
Fakultaet 4 = 0000000000000018
Fakultaet 5 = 0000000000000078
Fakultaet 6 = 00000000000002D0
Fakultaet 7 = 00000000000013B0
Fakultaet 8 = 0000000000009D80
Fakultaet 9 = 0000000000058980
Fakultaet 10 = 0000000000375F00
Fakultaet 11 = 0000000002611500
Fakultaet 12 = 000000001C8CFC00
Fakultaet 13 = 000000017328CC00
Fakultaet 14 = 000000144C3B2800
Fakultaet 15 = 0000013077775800
Fakultaet 16 = 0000130777758000 (*16 = ein HEX-Digit nach links)
Fakultaet 17 = 0001437EEECD8000
Fakultaet 18 = 0016BEECCA730000
Fakultaet 19 = 01B02B9306890000
Fakultaet 20 = 21C3677C82B40000
Fakultaet 21 = C5077D36B8C40000 (statt 2C5077D36B8C40000)
Fakultaet 22 = EEA4C2B3E0D80000 (statt 3CEEA4C2B3E0D80000)
Bei 21! und 22! sind nur die oberen HEX-Digits abgeschnitten.
Die restlichen HEX-Digits stimmen aber noch.
Leider kann man die gesuchte Zahl der Dezimalstellen nicht ohne Umwandlung in eine Dezimalzahl feststellen. Die Zahl den Endnullen könnte man zur Not auch berechnen.
Doch zur Umwandlung sehr großer Zahlen in unterschiedliche Zahlensysteme gibt es ein umfangreiches Online-Paket Binary Hex Converter, siehe Link im Download-Bereich.
Die beim Decimal to Hexadecimal Converter angegebene Einschränkung auf 19 Dezimalstellen scheint nicht zu stimmen, denn es funktionieren auch deutlich größere Zahlen damit korrekt.
Rekursiv berechnet ganz schön flott, aber halt nur bis 20!
Auf dem Scope sieht man schön, wie die Rechenzeit des ATmega328P in der Programmschleife mit z stetig steigt bis auf 463 µsec @16 MHz CPU-Takt für 20!
Das ist dank rekursiver Binär-Berechnung natürlich ein ganzes Stück schneller als bei der aufwendigen nachfolgend beschriebenen Dezimal-Methode für sehr große Fakultäten, die per s’AVR bei 20! aber auch nur 1,8 msec benötigt und somit ca. 3,9 mal langsamer ist als die rekursive Methode per GCC.
GCC benötigt per Dezimal-Methode dagegen 3,8 msec @16 MHz, ist bei 20! also um den Faktor 2,1 langsamer als s’AVR.
Außer dem grundsätzlichen Limit von maximal 20! (wegen 64 Bit für das Ergebnis) gibt es aber auch ein Limit durch die rekursiven Aufrufe, die mit einem ATmega328P und seinen 2048 bit SRAM bei 20! noch problemlos klappen (Stack-Bedarf abgeschätzt auf wenigstens 20 x 64 bit = 1280 bit). Mit weniger SRAM kann 20! mit der rekursiven Methode aber nicht funktionieren.
Jetzt auch noch per Arduino-IDE (5.1.2021)
Der Frust über die serielle Ausgabe bei GCC hat mich schließlich noch dazu verleitet, dasselbe Programm in Arduino-Umgebung zu realisieren.
Bekanntermaßen ist dort die serielle Ausgabe per serial.print noch spartanischer.
Aber in der Arduino-Library LibPrintf habe ich die Möglichkeit vermutet, die Ergebnisse vielleicht doch etwas komfortabler ausgeben zu können.
Das Einbinden der Library ging zunächst per Mausklick sehr einfach und schnell.
Allerdings muss man dann in der Arduino-Datei "platform.txt" (oder "platform.local.txt") bei den Einträgen "compiler.c.extra_flags" und "compiler.cpp.extra_flags" die bei den AVR-CPUs standardmäßig deaktivierte Unterstützung von "double double" per Compiler-Parameter
"–DPRINTF_PREVENT_DEFAULT_AVR_SETTINGS" erst wieder scharf machen (und danach die IDE neu starten), was das Anwendungsprogramm nach
#include <LibPrintf.h>
dann um einiges größer macht (wie auch bei GCC).
Das Ergebnis kann sich aber sehen lassen, denn printf funktioniert mit 64-bit-Zahlen jetzt perfekt wie es soll, sowohl dezimal als auch hexadezimal, ganz ohne Tricks!
printf("Fakultät %2d = %20llu", z, f);
Fakultät-Berechnung ...
Fakultät 1 = 1 Stellen: 1
Fakultät 2 = 2 Stellen: 1
Fakultät 3 = 6 Stellen: 1
Fakultät 4 = 24 Stellen: 2
Fakultät 5 = 120 Stellen: 3
Fakultät 6 = 720 Stellen: 3
Fakultät 7 = 5040 Stellen: 4
Fakultät 8 = 40320 Stellen: 5
Fakultät 9 = 362880 Stellen: 6
Fakultät 10 = 3628800 Stellen: 7
Fakultät 11 = 39916800 Stellen: 8
Fakultät 12 = 479001600 Stellen: 9
Fakultät 13 = 6227020800 Stellen: 10
Fakultät 14 = 87178291200 Stellen: 11
Fakultät 15 = 1307674368000 Stellen: 13
Fakultät 16 = 20922789888000 Stellen: 14
Fakultät 17 = 355687428096000 Stellen: 15
Fakultät 18 = 6402373705728000 Stellen: 16
Fakultät 19 = 121645100408832000 Stellen: 18
Fakultät 20 = 2432902008176640000 Stellen: 19
Auch die Anzahl der Ergebnisstellen fällt dabei per kleiner rekursiver Funktion mit ab.
Jetzt ist meine printf-Welt wieder in Ordnung, auch wenn die rekursive Binär-Berechnung von 20! mit der Arduino-IDE minimal langsamer ist (477 µs statt 463 µs).
Die klassische Methode (10.6.2019)
Möchte man noch größere Fakultäten exakt berechnen, z.B. 100! oder gar 1000!, wird man mit der oben gezeigten rekursiven Methode nicht weiter kommen und muss für die Darstellung aller Dezimalstellen zur klassischen Multiplikation "von Hand" greifen ("schriftliches Multiplizieren"), wie man es in der Grundschule gelernt hat. D. h. man erstellt pro Zehnerpotenz des jeweiligen z (z. B. 4-stellig, angefangen mit 1) ein eigenes (mit größer werdendem z sehr langes) Teilprodukt und addiert am Schluss alle Teilprodukte zum Zwischenergebnis, das man dann mit dem nächst größeren z multipliziert, u.s.w.
Aber schnell wird man erkennen, dass das Handrechnen bei so großen z-Werten recht mühsam ist, denn allein zum schnellen Niederschreiben des bekannten Ergebnisses von 1000! mit 2568 Stellen wäre man etwa 20 Minuten beschäftigt (bei kleiner Handschrift könnte eine DIN-A4-Seite damit ziemlich voll werden). Und selbst wenn man Tag und Nacht rechnen würde, wird ein Monat für das handschriftliche Berechnen von 1000! kaum reichen.
Man nimmt hierfür also besser einen schnellen Rechenknecht!
Ein moderner PC würde (je nach verwendeter Programmiersprache) das Ergebnis von 1000! in deutlich weniger als einer Zehntelsekunde berechnet haben. Mit einem 8-bit-Mikrocontroller dauert es aber schon etwas länger - vorausgesetzt, er hat auch genügend Arbeitsspeicher.
Und genau das wollen wir untersuchen, z.B. anhand eines ATmega1284, jenem 8-bit-AVR mit einem sehr großen Arbeitsspeicher[6] (nämlich 16 kByte), den es auch noch in handhabbaren Gehäusen gibt.
Diese "händische" Methode hatte ich auf dem PC bereits in den 90er Jahren mit QBasic und QuickC unter DOS versucht und gleich danach mit Pascal (Delphi 5) unter Windows, womit die Rechenzeiten drastisch kürzer wurden.
Letzteres ist heute noch meine Referenz, aber die einfache QuickC-Version für DOS soll mit einigen Erweiterungen zunächst als Basis für GCC und den ATmega1284 dienen, der bei meinen Untersuchungen mit 18 MHz getaktet wird.
Und so schaut das Quellprogramm in GCC aus (Kopie aus Atmel Studio), das fast beliebig große Fakuläten berechnet (bis der Speicher ausgeht):
[Hinweis: Auf Smartphones werden teilweise leider Inlineframes nicht richtig dargestellt. Deshalb erscheint dort der Quellcode in voller Länge und nicht in einem kleineren Scroll-Fenster.]
Wie im GCC-Quellprogramm am Ende erwähnt, benötigt der ATmega1284 zur Berechnung von 1000! in der ursprünglichen Version stolze 2:16 Minuten (mehr dazu siehe Ergänzung vom 30.6.2019).
Zur Berechnung anderer Fakultäten (z. B. 1227!, das Maximum für GCC auf dem ATmega1284) müssen im Quellprogramm bei Bedarf zwei Änderungen gemacht werden, nämlich unter Main der Wert für z:
factorial(1227);
und für optimale Speicherausnützung und kürzeste Laufzeit ganz am Anfang:
#define ExpLen 3260 // erwartete Anzahl der Ergebnisstellen von 1227!
Falls ExpLen unnötig groß gewählt wird, hat das nur den Nachteil längerer Laufzeiten oder im schlimmsten Fall stürzt das Programm ab (der Compiler streikt bei ExpLen>3269).
Das Hauptprogramm läuft in einer Endlosschleife. Die Laufzeit ist jene Zeit vom Erlöschen der LED bis zum nächsten Aufleuchten der LED.
Da bei meinen GCC-Untersuchungen eine einfache Platine mit ausschließlich dem ATmega1284 verwendet wurde und kein Display angeschlossen war, wurden zur Kontrolle nur die ersten 4 Digits des Ergebnisses per
PORTA = 16*fakul[ExpLen] + fakul[ExpLen-1];
und
PORTD = 16*fakul[ExpLen-2] + fakul[ExpLen-3];
ausgegeben und an den Pins nachgemessen (Low bzw. High per Voltmeter, Scope oder Logic-Analyzer). Die Werte "40" und "23" sind für 1000! ein sicheres Indiz, dass die Berechnung aller 2568 Stellen stimmt. Bei anderen Werten (insbesondere "00") ist etwas schief gelaufen.
Natürlich kann man je nach Lust & Laune und entsprechendem Hardware-Aufwand auch das per ATmega1284 berechnete Ergebnis auf irgendeinem Medium in seiner voller Länge einschließlich der vielen Endnullen ausgeben lassen. Per Laufschrift auf einer längeren 7-Segment-LED-Zeile (mit 500 msec Schrittzeit) wäre vielleicht eine Idee, um die eingangs erwähnten ca. 20 Minuten für eine Abschrift zu überprüfen ...
Tweaks
Die Abfragen von zd[j] und fakul[k] auf die Werte 0 und 1 bringen bereits eine große Steigerung bezüglich Rechengeschwindigkeit, da u. a. viele Multiplikationen entfallen.
Überraschenderweise hat aber der größere Aufwand, die indizierte FOR-Schleife
for (j = 0; j <= 3; j++)
zur Berechnung der Teilprodukte zu strecken ("Unrolling", "Unwinding") überhaupt keinen Laufzeitgewinn gebracht, so dass diese Methode im obigen GCC-Programm schließlich doch nicht angewendet wurde, wodurch das Programm natürlich deutlich kürzer und etwas übersichtlicher wird.
Aber: Der GCC-Compiler hat genau dieselbe Idee und wendet bei dieser FOR-Schleife zum Optimieren das Unrolling standardmäßig an - und deshalb gibt es keinen Unterschied zu meinem eigenen Versuch (den ich mir hätte schenken können, wenn ich die LSS-Datei des Compilers gleich angeschaut hätte)!
Strukturiert in AVR-Assembler programmiert (10.6.2019)
Jetzt geht es natürlich noch darum, die Ergebnisse von GCC mit s’AVR zu vergleichen.
Um wie beim GCC-Programm ebenfalls einen großen Laufzeitgewinn zu erzielen, muss man die Methode des "Entrollens" beim s'AVR-Programm also selbst umsetzen.
Das eigentliche s’AVR-Quellprogramm kann man entweder vom GCC-Quellprogramm ableiten, aber wegen der ähnlichen Syntax noch einfacher auch von einem Basic- oder Pascal-Programm (so man hat).
Nachfolgend schließlich das per Copy&Paste 4-fach gestreckte (und wie immer strikt strukturiert programmierte) s'AVR-Quellprogramm, das durch das Strecken zwar deutlich länger ist im Vergleich zu einer indizierten FOR-Schleife, aber dafür erstaunliche zehnmal schneller als das GCC-Programm unter sonst gleichen Bedingungen:
Softwaretricks (10.6.2019/11.2.2021)
Es ist aber nicht nur das Unrolling der genannten FOR-Schleife, sondern auch das trickreiche Anordnen und Berechnen der Teilprodukte, u. a. mit einem speziell hierfür entworfenen Macro MOD_DIV10, das die Einerziffern und den Übertrag in die nächste Dezimalstelle extrem schnell (ursprünglich in 10 Maschinenzyklen, per V1.1 auf 9 Maschinenzyklen reduziert) per MOD 10 und DIV 10 einer 8-Bit-Zahl (0..255) bestimmt, das im GCC-Programm den beiden Zeilen:
a = a / 10;
b = a % 10;
entspricht.
Hier das gesamte MOD_DIV10-Macro nebst ausführlicher Beschreibung (vielleicht kann das jemand für eigene AVR-Programme gebrauchen):
;=============================================================
; MOD_DIV10.mac
; AVR Assembler macro for MODULO and DIV
;
; written by Eberhard Haug, May 2019/February 2021
;
; License: GNU GENERAL PUBLIC LICENSE, Version 3, 29 June 2007
;
; Version: 1.1
;=============================================================
; MOD10 and DIV10 are typically used to convert binary to decimal,
; but also when adding decimal with carry
; To prevent divisions by 10, multiplications by 0.1 are used instead (state of the art).
; This can be done by multiplying by 205 (MUL) and dividing the result by 2^11 (using shifts).
; Intermediate steps are used to also get 10 * INT(n/10), which finally gets both MOD 10 and DIV 10.
; AVR ASM Procedure:
; 1. Multiply number in AKKU by 205, result in R1|R0 resp. PHI|PLO
; 2. MSByte (R1 resp. PHI) AND 0b11111000, which is equal 8 * INT(number/10) or 8 * DIV 10
; 3. separately 2 times LSR (/4) MSByte (R1 resp. PHI), which ends in 2 * DIV 10
; 4. add both and get 10 * DIV 10
; 5. subtract result from number, which results in number MOD 10 [in general: MOD(n, d) = n - d*INT(n/d)]
; 6. finally LSR (/2) result of item 3. to get number DIV 10 [in general: n DIV d = INT(n/d)]
.MACRO MOD_DIV10 ; input: number in AKKU, output: number MOD 10 in AKKU, number DIV 10 in CARRY
; PHI, PLO, AKKU, and CARRY are modified, no other registers must be saved
mul AKKU, C205 ; AKKU * 205 (from register), result in PHI|PLO
and PHI, BITP ; BITP = 0b11111000 (from register), PHI = 8 * number DIV 10
mov CARRY, PHI ; copy 8 * number DIV 10 to CARRY
lsr CARRY ; CARRY = 4 * number DIV 10
lsr CARRY ; CARRY = 2 * number DIV 10
add PHI, CARRY ; PHI = 10 * number DIV 10
sub AKKU, PHI ; AKKU = number MOD 10
lsr CARRY ; CARRY = number DIV 10
.ENDMACRO
Die Konstante 205 ist die größtmögliche 8-bit-Zahl (nämlich für maximale Genauigkeit), die sich durch Multiplikation von 0,1 mit einer 2er-Potenz ergibt, sprich 0,1 * 2^11 = 204,8, aufgerundet auf 205.
Damit ergibt sich 205/2^11 = 0,100097656, d. h. 1 ‰ bzw. 1/4 Bit Genauigkeit bei einem 8-bit-Wert. Dieses Macro bestimmt MOD10/DIV10 demnach exakt für alle 8-bit-Zahlen.
Interessant ist in diesem Zusammenhang vielleicht noch die Feststellung, dass die stellenweise Summe der vier Teilprodukte[1] bei 1000! nie größer als 29 ist.
Dieses (universell verwendbare) Macro belegt nur 8 Worte Programmspeicher pro Aufruf bzw. wegen 9 Aufrufen insgesamt 72 Worte für das gesamte s'AVR-Programm.
Im s'AVR-Hauptprogramm ist AKKU im oberen AVR-Registerbereich definiert, CARRY darf auch im unteren AVR-Registerbereich sein.
Das GCC-Programm benötigt für die reine Fakultätberechnung 728 Bytes, zzgl. 76 Bytes für das Unterprogramm (divmodhi4) für die MOD10/DIV10-Berechnung. Das ist zwar etwas sparsamer als ein vielfach verwendetes Macro, aber bei häufigen Aufrufen deutlich langsamer.
Beim s'AVR-Programm sind es für die reine Fakultätberechnung 330 Bytes inklusive der neun MOD_DIV10-Macros für die Fakultätberechnung.
Insgesamt ist das GCC-Programm (nur die eigentliche Fakultätberechnung!) also mehr als doppelt so groß wie das s'AVR-Programm.
Beim s'AVR-Programm kann man die zu berechnende Fakultät in einer Definitionsdatei zwischen 100!, 500!, 1000! und 1230! auswählen und die diversen Programmvariablen werden vom Assembler automatisch angepasst.
Außerdem werden beim s'AVR-Programm die ersten 8 Digits des Ergebnisses, die Anzahl der Ergebnis-Digits und die Zahl der Endnullen (beides per Programm aus dem Ergebnis ausgezählt) auf einem TM1640-basierenden[2] 16-Digit-LED-Display dezimal dargestellt, hier für 1000!:

Auch hier läuft das Hauptprogramm nach dem ersten Berechnen und Anzeigen in einer Endlosschleife zum Messen der Laufzeit, wiederum ab Erlöschen der LED bis zum nächsten Aufleuchten der LED.
Um den Arbeitsspeicher maximal zu nützen (nämlich 99,8%), kann man mit dem s'AVR-Programm bis zu 1230! mit 3269 Stellen in ca. 21 Sekunden berechnen.
Beim GCC-Programm ist aufgrund eines größeren SRAM/Stack-Bedarfs nur maximal 1227! mit 3260 Stellen (und 304 Endnullen) möglich (Laufzeit 3:19 Minuten).
Fazit s’AVR vs. GCC
Im Vergleich zum GCC-Programm zur Berechnung von sehr großen Fakultäten (z. B. 1000!) auf einem ATmega1284 ist das vorgestellte s'AVR-Programm zirka zehnmal schneller und benötigt dabei nur etwa 41% des Programmspeichers. Bei beiden Programmen wird dabei derselbe Berechnungsalgorithmus angewendet.
Der C-Compiler verwendet (grundsätzlich) ungeschickterweise für die Konstante 0[3] das AVR-Register R1, das aber (neben R0) bei vielen AVR-CPUs auch für die Multiplikation verwendet wird. Das Retten bzw. Neubeschreiben von R1 mit dem Wert 0 kostet unnötig Zeit.
Bei vergleichsweise ähnlich guter strukturierter Programmierung wie bei GCC kann man per s’AVR aber alle Spezialitäten der AVR-CPU berücksichtigen und damit einige Fallstricke umgehen.
So habe ich zwar für schnelle Zugriffe und optimale Ausnützung der oberen AVR-Register ebenfalls einige Konstante in den weniger flexiblen unteren AVR-Registern abgelegt, aber R0 und R1 natürlich für die Multiplikation freigehalten, die im vorgestellten Programm sehr häufig[4] aufgerufen wird.
Auch das ausgefeilte MOD_DIV10-Macro (das ebenfalls eine Multiplikation enthält) trägt zum Laufzeitgewinn bei.
Und schließlich erlaubt das im s’AVR-Programm angewandte Verschachteln von Zwischenergebnis und den vier Teilprodukten in einem einzigen großen Array die elegante Adressierung aller Arrays gleichzeitig mit nur einem Pointer-Register und per Displacement, das bei AVR leider nur einen kleinen Bereich von 0 bis 63 zulässt und deshalb bei fünf separaten Arrays für das sehr lange Zwischenergebnis und die ebenso langen vier Teilprodukte nicht angewendet werden könnte.
Bestimmt gibt es beim vorgestellten GCC-Programm noch ein paar Details zu verbessern, um kürzere Laufzeiten zu erzielen. Aber eine Steigerung um den Faktor 10 scheint mir nicht machbar.
Überraschend ist vielleicht noch die Tatsache, dass der gestreckte s’AVR-Quellcode für die reine Fakultät-Berechnung nur knapp über dreimal so viele Programmzeilen benötigt wie der ungestreckte GCC-Quellcode. So betrachtet, wäre das s’AVR-Quellprogramm sogar noch etwas kompakter als das GCC-Quellprogramm.
Ziemliche GCC-Beschleunigung durch ein kleines Detail (30.6.2019)
Nun schien der Laufzeitunterschied zwischen GCC und s’AVR doch etwas sehr groß, so dass ich das ursprünglich für den PC geschriebene GCC-Programm nochmals genauer angeschaut habe.
Und siehe da, eine kleine Änderung bei der Definition zweier Variablen ergibt einen sehr großen Schritt nach vorn, auch wenn beim Ergebnis immer noch ein deutlicher Abstand zu s’AVR übrig bleibt (und nun der Laufzeitvergleich ähnlich wie bei der Ackermann-Funktion ausfällt):
// int a, b; // Zwischenwerte bei der Fakultät-Berechnung
uint8_t a, b; // Zwischenwerte bei der Fakultät-Berechnung
Die großen Arrays fakul[ExpLen+3] und tp[4][ExpLen+3] wurden von Anfang an als 8-Bit-Variable definiert, denn sonst wäre die Berechnung von 1000! aufgrund des begrenzten Arbeitsspeichers des ATmega1284 überhaupt nicht möglich gewesen.
Überraschend, dass der GCC-Compiler bei den Variablen a und b bei der ursprünglichen Definition "int a, b;" keine Optimierung gefunden hat.
Mit dieser kleinen Änderung wird vom GCC-Programm deutlich mehr Programmspeicher belegt (nämlich nun 946 Bytes für die reine Fakultätberechnung), da statt dem Unterprogramm divmodhi4 bis auf ein einziges Mal nun (wie bei s’AVR) immer eine offensichtlich Macro-basierende Befehlsfolge eingefügt wird.
Schließlich beträgt die GCC-Laufzeit für 1000! jetzt ca. 25 sec und ist bei 2,9-fachem Programmspeicherbedarf somit "nur" noch um den Faktor 1,8 langsamer als das s’AVR-Programm.
Berechnungen auf kleineren ATmegas mit serieller Ausgabe (30.12.2020)
Inzwischen habe ich die obigen Programme angepasst für eine elegantere serielle Ausgabe per USART, so dass man die Ergebnisse vollständig per Terminal-Software (z. B. HTerm) anschauen kann und nicht nur einen kleinen Teil auf einer 7-Segmentanzeige sieht oder gar Port-Pins ausmessen muss.
Das funktioniert besonders einfach, wenn man ein Arduino-Board (UNO oder nano) verwendet, da dort die serielle Schnittstelle von Windows aus per USB bzw. COMx ansprechbar ist.
Man muss sich dabei halt bewusst sein, dass jede zusätzliche Library in C-Umgebung extra Resourcen frisst. Dabei ist der Programmspeicher sicher nicht das Problem, aber das SRAM, das man für die Berechnungen benötigt.
Um das umzusetzen, habe ich für GCC allerdings erst mit etwas Aufwand die formatierte Druckfunktion printf einbinden müssen, da diese unter Atmel Studio leider nicht standardmäßig unterstützt wird.
Bei scanf habe ich jedoch nach einigen misslungenen Versuchen aufgegeben. Deshalb ist bei meinen Programmen unter GCC derzeit keine Deluxe-Eingabe der zu berechnenden Fakultät per Terminal möglich, sondern weiterhin nur per konstantem (aber wählbarem) Programm-Parameter.
Auf einem ATmega328P mit nur 2 kByte SRAM kann per GCC mit der oben beschriebenen Dezimal-Methode maximal 192! berechnet werden.
Die Ausgabe auf HTerm schaut dann z. B. so aus:
Das Ergebnis von 192! liegt vollstaendig vor:
354996793146960497053355363383973425965094809743694
491885455534984190204750249968830591340591162785093
141951525209177997501478084577063512837513105442388
103085116949108248219929177667335850225156399124325
817472036634653562449665740610033707601842063277098
323069015230061026956365247457276593902258859903874
498560000000000000000000000000000000000000000000000
192! hat 357 Stelle(n) und 46 Endnull(en).
Per s’AVR ging mir das Ganze programmiertechnisch deutlich schneller und einfacher von der Hand, dann mit dieser Terminal-Ausgabe:
Berechnung von 192!
354996793146960497053355363383973425965094809743694
491885455534984190204750249968830591340591162785093
141951525209177997501478084577063512837513105442388
103085116949108248219929177667335850225156399124325
817472036634653562449665740610033707601842063277098
323069015230061026956365247457276593902258859903874
498560000000000000000000000000000000000000000000000
Stellen: 357
Endnullen: 46
Bei noch weniger SRAM wird es natürlich eng mit der Fakultät-Berechnung. Bei 1 kByte SRAM schätze ich maximal 120! per s’AVR und per GCC entsprechend noch weniger.
Laufzeiten
Inzwischen habe ich die Berechnungen auf drei Teilprodukte verkürzt, wenn weniger als 1000! berechnet werden soll.
Dann benötigt s’AVR für diese Berechnungen bei 16 MHz CPU-Takt nur 314 msec (sonst 361 msec) und GCC dagegen 573 msec (sonst 644 msec), alles nun etwas genauer per Scope gemessen. Das ist mit 1,82 etwa dasselbe Verhältnis GCC/s’AVR wie bei den größeren Fakultäten auf dem ATmega1284.
Da die serielle Schnittstelle bei meiner Umsetzung per s’AVR das SRAM während der Fakultäts-Berechnung nicht extra belastet, lässt sich damit sogar bis zu 212! berechnen, dann in 391 msec (sonst 451 msec bei 4 Teilprodukten).
Mit dem geringfügig beschleunigten MOD_DIV10 benötigt 212! nur noch 384 msec (12.02.2021).
Algorithmus verbessern? (10.6.2019)
Den Berechnungs-Algorithmus könnte man für alle Programme noch insoweit verbessern, dass man die Teilprodukte nicht immer über die volle Länge berechnet, sondern - ähnlich wie beim Rechnen mit Papier und Bleistift - mit einem dynamischen Pointer beim Zwischenergebnis nur bis zur höchsten Ziffer <> 0.
Da aber bei den Teilprodukten bereits grundsätzlich auf die Ziffern 0 und 1 abgefragt wird, bringt eine solche Vorgehensweise vielleicht nicht allzu viel Laufzeitgewinn.
SRAM sparen für noch größere Fakultäten (31.12.2020)
Um SRAM für die Zwischenrechnungen zu sparen, könnte man grundsätzlich nur Platz für ein statt vier Teilprodukte vorsehen, dann weiteren Teilprodukte dort aufaddieren und erst am Schluss das Teilproduktfeld ins Ergebnisfeld.
Da der Rechenaufwand hierfür einiges größer ist, wird die Laufzeit zur Berechnung gleicher Fakultäten entsprechend länger.
Für den ATmega328P wage ich die Aussage, dass man mit dieser komplizierteren Methode per s’AVR maximal 450! berechnen.
Anstatt bei der Multiplikation einen Multiplikator mit vier einzelnen Dezimalziffern könnte man schließlich auch einen 16-bit-Binärwert verwenden und dann die Produkte der einzelnen Dezimalstellen direkt im Ergebnisfeld aufaddieren, so dass fast das gesamte SRAM für das Ergebnisfeld zur Verfügung steht, womit man per ATmega328P vielleicht sogar mehr als 820! berechnen kann.
Untersucht habe ich das bislang aber nicht.
Kein großer Gewinn (16.6.2019)
Zwischendurch habe ich mit meinem Delphi-Programm ein Verfahren untersucht, das das Berechnen der Teilprodukte abkürzt, sobald eine führende Null beim Zwischenergebnis erreicht wird, mit dem Ergebnis, dass es (bedingt durch zusätzliche Abfragen) nur dann einen signifikanten Laufzeitgewinn gibt, wenn die Arrays deutlich größer sind als für die jeweilige Fakultät unbedingt nötig wäre.
Deshalb werde ich mir diesen extra Aufwand bei den AVR-Programmen sparen, da die Programme dadurch umfangreicher werden und nicht mehr so übersichtlich sind.
Nur knapp schneller mit Delphi und i5-CPU
Das erwähnte, aber hier nicht im Detail beschriebene Pascal/Delphi-Programm gibt nicht nur das Ergebnis von bis zu 2000! (bei Bedarf und Neukompilierung sogar bis 9999! [5]) in voller Länge auf dem Bildschirm aus, sondern bestimmt auch die Anzahl der Ergebnisstellen und der Endnullen, ebenso die Laufzeit.
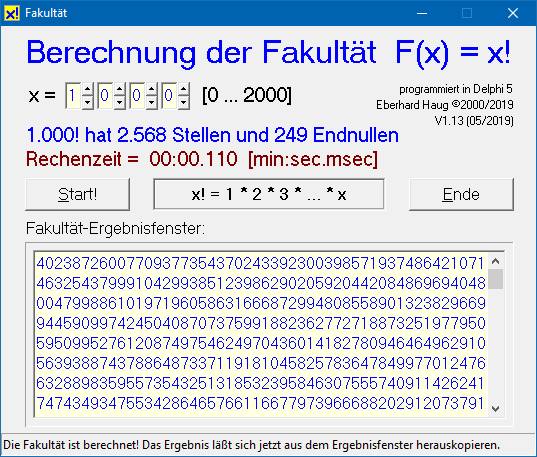
Dieses Delphi-Programm benötigt mit demselben Berechnungsalgorithmus für 1000! bei optimierten Array-Größen (oder einem dynamischem Pointer, siehe Anmerkung vom 16.6.2019) und einer i5-CPU @3,3 GHz nur 64 msec (sonst ca. 110 msec).
Umgerechnet auf die 18 MHz des ATmega1284 dürfte dieser für 1000! demnach 11,7 sec benötigen.
So gesehen sind die mit dem s'AVR-Programm erzielten 14 Sekunden @18 MHz schon ziemlich nahe dran, das GCC-Programm ist mit 2:18 Minuten (per int a, b;) bzw. 25 Sekunden (per uint8_t a, b;) Laufzeit für dieselbe Berechnung aber deutlich abgeschlagen.
In diesem Fall der "händischen" Berechnung einer großen Fakultät gewinnt eben die 64-bit-CPU trotz Hardware-Dividierer nur knapp gegen den kleinen 8-bit-Mikrocontroller, der sich aber bei geschickter Programmierung trotzdem ganz wacker schlägt.
Bei Interesse kann das Delphi-Programm für Windows (WIN98SE bis WIN10) gerne als EXE- oder ZIP-Datei zur Verfügung gestellt werden.
Die Profis
Wenn man richtig viel Rechen-Power nebst großem Arbeitsspeicher und geeignete Mathe-Libraries zur Verfügung hat, lassen sich (extrem) große Fakultäten mit ziemlich ausgefeilten Methoden auch noch schneller berechnen. Diese sind aber für einen kleinen 8-bit-Mikrocontroller nicht mehr geeignet.
Turbo-Fakultät per kombinierter Binär/Dezimal-Multiplikation (25.1.2021)
Kürzlich baten mich gleich zwei Besucher meiner Website um Stellungnahme zu einem Programm zur Berechnung großer Fakultäten auf einem ATmega. Dieses Programm hatte die weiter oben angedeutete kombinierte Binär/Dezimal-Multiplikation umgesetzt (die ich mir eigentlich schenken wollte), die eine Geschwindigkeitssteigerung verspricht und vor allem bei gleicher Fakultät deutlich weniger RAM für das Berechnungsfeld benötigt.
Beim genaueren Recherchieren bin ich dann auf die (offensichtlich) ursprüngliche Quelle[7] in C-Sprache gestoßen.
Dort wird mit wenig Programmieraufwand nicht nur schneller multipliziert, sondern ganz clever dynamisch die Stellenzahl bestimmt, so dass immer nur so viele Dezimalstellen multipliziert werden, wie unbedingt nötig.
Ich habe dieses Programm für möglichst wenig Stack-Bedarf vereinfacht, wodurch bei limitiertem RAM sogar etwas größere Fakultäten berechnet werden können, und vor allem noch schneller, da ein zusätzlicher Funktionsaufruf für die eigentliche Multiplikation entfällt:
void fakultaet (int n) // die Fakultät von n (= n!) ist zu berechnen
{
Ergebnis[0] = 1; // den ersten Ergebnis-Eintrag (Multiplikant)
// mit 1 vorbelegen
stellen = 1; // die zugehörige Stellenzahl ist ebenfalls 1
for (int x = 2; x <= n; x++) // x = 2 ist der erste Multiplikator
{
int carry = 0; // den Übertrag als 16-bit-Binärwert initialisieren
for (unsigned short i = 0; i < stellen; i++) // ziffernweise Multiplikation aller vorhandenen
{ // Dezimal-Digits von Ergebnis[i]
int produkt = Ergebnis[i] * x + carry; // das akkumulierte Produkt wird allerdings
// als 16-bit-Binärzahl dargestellt
Ergebnis[i] = produkt % 10; // Abspeichern des 10er-Rests immer an höchster Stelle
carry = produkt / 10; // der ganzzahlige Anteil ist der neue Übertrag
}
while (carry) // den Übertrag weiterer 10er-Reste als weitere
{ // Dezimal-Digits in Ergebnis[stellen] ablegen
Ergebnis[stellen] = carry % 10;
carry = carry / 10;
stellen++; // für jeden weiteren gefundenen 10er-Rest
} // die Stellenzahl um eins erhöhen
}
}
Das ist nun ein wirklich sehr einfaches und sehr überschaubares C-Programm, das immerhin 760! mit seinen 1.862 Stellen und 189 Endnullen auf einem ATmega328P in 9,66 sec berechnen kann.
Zum Vergleichen mit den bisherigen Berechnungsmethoden hier auch noch die Laufzeiten für 192!, dem Maximum per GCC mit der reinen Dezimal-Methode (@16 MHz):
Der Geschwindigkeitsgewinn beträgt mit der kombinierten Binär/Dezimal-Methode bei GCC dennoch nur 20%, und selbst gegenüber der reinen Dezimal-Methode per s’AVR ist GCC mit der schnelleren Binär/Dezimal-Methode immer noch um 45% langsamer.
Zunächst dachte ich, man könnte das wie bei der reinen Dezimal-Methode durch Abfragen von ergebnis[i] auf Werte von 1 und 0 etwas beschleunigen (0 ist wegen den Endnullen häufiger als 1). Das ist aber eindeutig nicht der Fall, da die zusätzlichen Abfragen bei jedem Dezimal-Digit mehr Zeit kosten als geringfügig schnellere Berechnungen ohne Multiplikation, siehe Tabelle.
Doch noch deutlich schneller möglich (17.2.2021)
Beim Verbessern der Binär/Dezimal-Methode für extrem große Fakultäten (bis 5015!) auf dem ATmega1284P konnten die Laufzeiten deutlich verkürzt werden.
So wird damit 192! in ca. 86 msec @18 MHz (bzw. in 97 msec @16 MHz, statt 231 msec in der Tabelle) berechnet.
Aufsteigend mit Vorteil (25.1.2021)
Wie man an der FOR-Schleife des GCC-Programms erkennt, wird die Fakultät mit aufsteigenden Multiplikatoren berechnet, was gegenüber absteigenden Werten besonders bei kleineren Fakultäten einen deutlichen Vorteil bringt, da die Teilergebnisse am Anfang weniger Stellen haben, so dass man insgesamt sehr viel weniger Multiplikationen benötigt. Erst bei sehr großen Fakultäten relativiert sich das Ganze.
In der folgenden Tabelle ist jeweils die Summe der per FOR-Schleife bearbeiteten Dezimal-Stellen angegeben (per Delphi-Programm ermittelt).
Pro Stelle wird allein für jedes Teilprodukt eine 16-bit-Binär-Multiplikation durchgeführt:
Damit dieser Vorteil auch beim s’AVR-Programm zum Tragen kommt, wurde extra das Register-Paar YH:YL geopfert, um für die Fakultäts-Berechnung trotz ansteigenden Multiplikatoren im Register-Paar XH:XL einen schnellen Schleifenzähler zu bekommen, der bei den AVR-µC vorteilhaft per Dekrement (sbiw YH:YL,1) realisiert wird, da man abschließend auf Null abfragen kann und für größere Fakultäten nicht jedesmal einen 16-bit-Vergleich durchführen muss.
Volles Werk mit s’AVR
Um die Binär/Dezimal-Methode per s’AVR für möglichst kurze Rechenzeiten umzusetzen, musste ich beim ATmega328P wirklich alle Register ziehen:
Allerdings ist das s’AVR-Programm aufgrund der umfangreichen Kommentare jetzt nicht mehr ganz so kurz und knackig wie das direkt vergleichbare GCC-Programm - aber doppelt so schnell, siehe obige Tabelle.
Noch einen Kick beschleunigen könnte man, indem Bin16Dez linear als Teil von factorial geschrieben wird und nicht als Unterprogramm.
Der besseren Übersichtlichkeit wegen habe das aber separat belassen und zum besseren Verständnis ist zwischendrin noch etwas Pascal- und C-Code als Kommentar mit aufgeführt.
Bin16Dez
Einen Anteil daran hat das Unterprogramm Bin16Dez, das auf eine etwas unübliche Art und Weise (siehe Quellenangabe in Source-Code) 16 Bit von NUM1:NUM0 ziemlich flott in vier Dezimal-Digits DEZ3:DEZ2:DEZ1:DEZ0 umwandelt.
Da die Binär/Dezimal-Methode per s’AVR die Teilprodukte und Überträge mit 16 Bit akkumuliert (damit auch deutlich größere Fakultäten von z. B. 5000! auf einem ATmega1284 berechnet werden können) muss man bei Bedarf ab 960! noch ein weiteres Dezimal-Digit DEZ4 oder stattdessen das Register CARRY verwenden, siehe obigen Quell-Code.
Zum besseren Verständnis wurde der Originaltext der Quelle und ein C-Code mit angegeben, der nahezu 1:1 in s’AVR-Sprache umgesetzt wurde, wobei jetzt auch das bereits früher verwendete sehr schnelle Macro MOD_DIV10 mehrfach zum Einsatz kommt.
Kein weiteres MOD_DIV10 für den Überlauf
Im C-Code für die Fakultät wird nach Abarbeitung aller Stellen in der While-Schleife der Überlauf der Multiplikationen auf weitere Dezimal-Digits verteilt, wofür dort %10 und /10 benötigt wird.
Da im s’AVR-Code mit der Funktion Bin16Dez aber der Überlauf bereits in Form von Dezimal-Digits vorliegt, muss man diese nur noch im Ergebnisfeld per einfacher IF-Schleife der Reihe nach verteilen und benötigt keine weiteren Multiplikationen! Vermutlich bringt dieses Detail neben dem schnellen MOD_DIV10 bereits einen Laufzeitgewinn.
Extra Fakultäten
Da das s’AVR-Programm im Vergleich zu GCC nicht ganz soviel Stack für die serielle Ausgabe benötigt, lässt sich damit per ATmegaA328P sogar 822! in 5,85 sec @16 MHz berechnen, ohne dass das Ergebnisfeld (endet direkt unter dem Stack!) bei der Ausgabe überschrieben wird.
Zum Vergleich: Für 760! werden per s’AVR nur 4,92 sec benötigt, statt 9,66 sec per GCC.
Auch hierfür wiederum doppelt so schnell.
Noch einen Kick schneller
Falls Bin16Dez innerhalb von factorial (und nicht wie oben als Unterprogramm) geschrieben wird, sind es sogar nur 4,68 sec für 760!
Allerdings muss man dann den Sprungbereich der beiden REPEAT-Schleifen per REPEAT.m erweitern (wodurch vom s’AVR-Precompiler bei UNTIL Z für den Rücksprung jeweils automatisch RJMP-Befehle generiert werden).
Hier ein Auszug der äußeren REPEAT-Schleife aus dem erzeugten flachen AVR-Assembler-Programm:
adiw XH:XL,1 ; FACT := FACT + 1 (which is 2)
;01// REPEAT.m ; the 16-bit FOR loop is handled by REPEAT-UNTIL
_AL163:
.
.
.
adiw XH:XL,1 ; FACT := FACT+1
sbiw YH:YL,1 ; decrementing REPEAT loop counter (originaly FOR)
;01// UNTIL Z
BREQ _AL165
RJMP _AL163
_AL165:
ret
Der von s’AVR erzeugte BREQ-Befehl zum Überspringen des RJMP-Befehls ist keinesfalls "schlechter" als ein (bei AVR nicht vorhandener) SKIP-Befehl, aber es muss halt vom Precompiler ein Label erzeugt werden.
Den erzeugten Code etwas durchleuchtet (1.2.2021)
Nun habe ich doch noch den von GCC generierten AVR-Assembler-Code in der LSS-Datei etwas näher angeschaut und mit dem s’AVR-Code verglichen.
Die reine Fakultät-Berechnung benötigt per GCC 210 Byte (gegenüber 728 Byte bei der reinen Dezimalmethode). Dazu kommen 78 Byte für das Unterprogramm divmodhi4, sprich insgesamt 288 Byte.
Bei s’AVR sind es für die reine Fakultät insgesamt 161 Byte. Davon sind 96 Byte für die Umwandlung Bin16Dez, in dem auch 5x das Macro MOD_DIV10 enthalten ist (das in etwa divmodhi4 entspricht).
Das heißt, GCC benötigt jetzt nur noch den 1,8-fachen Programmspeicher (statt ursprünglich 2,9-fach bei der reinen Dezimalmethode, beide Programme mit 4-fach-Unrolling). Am Geschwindigkeitsverhältnis hat es aber etwas eingebüßt.
Alle 216 Binärzahlen werden richtig flott konvertiert
Die Umwandlungs-Routine Bin16Dez habe ich mittlerweile für alle 16-bit-Zahlen in einer Programmschleife von 0 bis 216-1 mit einer sehr viel langsameren (und bewährten) Subtraktions-Methode verglichen, um sicher zu gehen, dass alle Konvertierungen stimmen.
Bei dieser Gelegenheit habe ich aus der per Scope gemessenen Zeit pro 16-bit-Schleife die durchschnittliche Anzahl der CPU-Zyklen pro 1x Bin16Dec auf 85 (ohne abschließenden RET-Befehl) überschlagen, und zwar sowohl für alle Zahlen als auch separat nur für die untere Hälfte von 0 bis 215-1.
Beim genauen Auszählen der Zyklen anhand des Quellprogramms waren es ohne Überlauf bei DEZ0 tatsächlich 86 CPU-Zyklen, aber theoretisch bis zu 105, wenn alle AVR-Befehle bei Überlauf der niedrigsten Ziffer DEZ0 gezählt werden.
Bei den Ziffern DEZ1 bis DEZ3 (oder ggf. DEZ4) sind die Produktterme immer ≤ 225.
Bei der Berechnung von DEZ0 kommt der Überlauf (>255) ausschließlich in der oberen Hälfte (nämlich ab 49.146) vor und dort nur relativ selten.
Deshalb macht es bei der durchschnittlichen Anzahl von CPU-Zyklen pro Konvertierung so gut wie keinen Unterschied.
Mit anderen Worten:
Die verwendete reine 16-Bit-Binär/Dezimal-Wandlung wird in den meisten Fällen in ca. 5,4 µsec @16 MHz durchgeführt[8].
Per Scope wurden dann noch mit einem anderen Setup zwischen zwei I/O-Pin-Flanken direkt vor und nach dem Unterprogrammaufruf (also zusätzlich 7 Zyklen für RCALL/RET und 2 Zyklen für 1x I/O) überwiegend 6,01 µsec und dann noch die selten Ausreißer bis ca. 6,75 µsec gemessen.
Hier die zugehörige Hüllkurve für alle Zahlenwerte 0 bis 216-1:
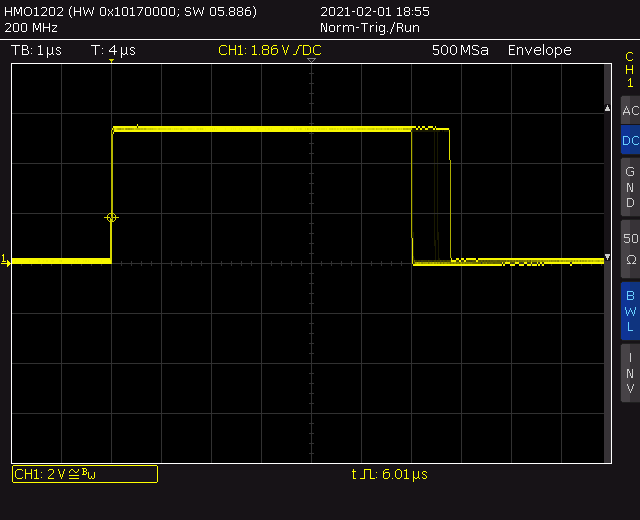
Mit gutem Auge erkennt man zwischen der minimalen und maximalen Messzeit noch zwei weitere Flanken, die zu dieser weiteren Abfrage bei DEZ0-Überlauf gehören:
IF AKKU >= #10
subi AKKU, 10 ; DEZ0 := DEZ0 - 10
inc CARRY ; CARRY := CARRY + 1
ENDI
Diese zusätzliche Abfrage auf ≥10 wird noch weggetunt, siehe folgenden Beitrag.
Bin16Dez noch etwas getunt (3.2.2021)
Die Carry-Abfrage bei der niederwertigsten Stelle DEZ0 (das Carry wird grundsätzlich nur bei Binärwerten ab 49.146 gesetzt) habe ich nun etwas vereinfacht.
Ursprünglich lautete die Carry-Abfrage so:
IF C
MOD_DIV10 ; input: number in AKKU, output: number MOD 10 in AKKU, number DIV 10 in CARRY
ldi AKKU2, 25
add CARRY, AKKU2 ; CARRY := CARRY + 25
add AKKU, AKKU3 ; DEZ0 := DEZ0 + 6
IF AKKU >= #10
subi AKKU, 10 ; DEZ0 := DEZ0 - 10
inc CARRY ; CARRY := CARRY + 1
ENDI
ELSE
MOD_DIV10 ; input: number in AKKU, output: number MOD 10 in AKKU, number DIV 10 in CARRY
ENDI
Falls die Addition von 6 [9] bereits vor MOD_DIV10 erfolgt, wird ein eventueller 10er-Überlauf gleich mit abgedeckt und somit die weitere Abfrage und Korrektur vermieden:
IF C ; simplified code ...
; due to C=256 we got a carry of 25 (256/10) and a remainder of 6 (256%10),
; AKKU is the modulo 256 remainder of d0
; obviously we got 370 such cases (can be detected if 6 is not added)
subi AKKU, -6 ; DEZ0 := DEZ0 + 6
MOD_DIV10 ; input: modulo 256 remainder + 6 in AKKU,
; output: number MOD 10 in AKKU, number DIV 10 in CARRY
ldi AKKU2, 25 ; INT(256/10)
add CARRY, AKKU2 ; CARRY := CARRY + 25 (instruction subi does not work for register CARRY
; being located in the lower register area)
ELSE
MOD_DIV10 ; input: number in AKKU, output: number MOD 10 in AKKU, number DIV 10 in CARRY
ENDI
Das entspricht zwar nicht mehr ganz dem Original von Douglas W. Jones, ist bei DEZ0-Überlauf jetzt aber nur noch konstant zwei Taktzyklen langsamer als ohne Überlauf (sofern man so große Zahlen bei kleineren Fakultäten überhaupt wandeln muss).
Auf dem Scope schaut die Hüllkurve für alle 216 Zahlen dann so aus (bereits mit der etwas beschleunigten Version 1.1 von MOD_DIV10):

Damit gibt es nur noch zwei unterschiedliche Messzeiten, nämlich 5,76 µsec (für mehr als 99% aller Zahlen) und ca. 6 µsec bei Überlauf während der Berechnung der Stelle DEZ0 (für nur 370 Zahlen ≥49.146).
Inzwischen habe ich auch noch den bezüglich Überlauf bei DEZ0 "optimierten" C-Code von Douglas W. Jones fehlerfrei auf dem ATmega328P laufen lassen, der pro Konvertierung per GCC 9,58 µsec bzw. 9,83 µsec @16 MHz benötigt, sprich ca. 1,7 mal langsamer ist als mein äquivalentes s’AVR-Programm.
5000! mit dem ATmega1284P (17.2.2021)
Nachdem jetzt programmtechnisch alles gut vorbereitet ist, muss natürlich auch noch der ATmega1284P mit seinem größeren SRAM für die kombinierte Binär/Dezimal-Methode herhalten.
Für 5000! mit 16.326 Ergebnisstellen (und 1.249 Endnullen) passt das bei 16.384 Bytes SRAM auf jeden Fall noch mit ausreichend Reserve für die serielle Ausgabe, die bei meiner ATmega1284P-Platine nun mit einem FT232-basierenden Stick per Terminal-Window am PC angeschlossen ist (statt dem ursprünglichen TM1640-Display), so dass jetzt auch das Ergebnis sehr großer Fakultäten vollständig sichtbar (und einfacher überprüfbar) gemacht werden kann.
Allerdings muss für so große Fakultäten bei Bin16Dez auch noch CARRY als 5. Dezimalstelle "DEZ4" mit ausgewertet werden, denn z. B. die letzte Multiplikation ist immerhin 5.000*8 = 40.000.
Es gibt aber noch deutlich größere Teilprodukte, vor allem da dort auch der vorausgegangene Übertrag akkumuliert wird. 16 Bit reichen aber immer noch aus.
Da eine weitere Stelle beim Übertrag auf der Dezimalseite durch das Hin- und Herkonvertieren sehr viel Rechenzeit benötigen würde (so praktisch das Aufteilen der Dezimalstellen ist), wurde jetzt sowohl das 8x16-Produkt nebst Akkumulation im Doppelregister NUM1:NUM0 als auch die Übertragsberechnung in CARRYH:CARRYL vollständig auf der Binärseite durchgeführt, sprich ein schnelles 16bit-MOD/DIV10 musste dafür geschrieben werden.
Bei dieser Gelegenheit wurden noch einige weitere Programm-Details verbessert, die die Laufzeiten deutlich verkürzen. Lediglich die Binär/Dezimalwandlung Bin16Dez ist noch dieselbe geblieben (wenn auch nicht maximal schnell[8], so doch wegen des Algorithmus schön).
Programmiertechnisch betrachtet, ist das s’AVR-Programm dem GCC-Programm damit sehr ähnlich.
Das Ergebnis von 5000! wird per s’AVR in 1:46 Minuten Laufzeit @18 MHz berechnet. Dabei werden (wie bei den folgenden Zeitangaben) Bin16Dez und MOD16DIV10 der Übersichtlichkeit wegen beim s’AVR-Programm als Unterprogramme aufgerufen (was etwas Laufzeit kostet).
Bis auf das letzte SRAM-Byte
Die maximal mit dem ATmega1284P vollständig berechenbare Fakultät liegt aufgrund des verfügbaren SRAMs bei 5015!, die vom s’AVR-Programm in 1:47 Minuten berechnet wird.
Bei 16.382 Stellen (= 216 -2) für das Ergebnis[10] (mit 1.252 Endnullen) bleiben dann noch genau zwei Bytes für den finalen Rettungssprung aus dem Fakultäts-Unterprogramm per RET zurück ins Hauptprogramm - optimaler geht es nicht!
Kombiniert Binär/Dezimal per s’AVR fast so schnell wie rekursiv per GCC
Statt den 463 µsec @16 MHz für 20! mit der oben beschriebenen flotten rekursiven Methode (die allerdings absteigend arbeitet, was aber bei der binären Berechnung keine Rolle spielt), sind es mit der Binär/Dezimal-Methode per s’AVR 537 µsec @18 MHz bzw. 600 µsec @16 MHz, also nicht viel langsamer als GCC mit der rekursiven Methode, die aber halt nur bis 20! statt bis zu 5015! geht.
Im Vergleich zum Delphi-Programm auf dem PC mit der Binär/Dezimal-Methode (siehe nächsten Beitrag) ist 5000! per s’AVR dagegen etwa 1,75 mal langsamer (auf dieselbe CPU-Frequenz normiert). Jetzt ist die CPU des PCs durch die größere Wortbreite beim Multiplizieren und Dividieren deutlich überlegen.
Per GCC klappt 5000! wegen knapp zu wenig SRAM auf dem ATmega1284P leider nicht.
Aber nachdem alle int auf uint16_t geändert wurden, klappt immerhin 4960! in 2:20 Minuten. Dieselbe Fakultät "schafft" s’AVR in 1:44 Minuten (beide Werte @18 MHz), ist also nur noch um den Faktor 1,35 schneller als GCC. Offensichtlich hat GCC ebenfalls ein schnelles 16-bit-MOD/DIV10.
Nicht viel schneller (21.2.2021)
Es war einen Versuch wert, mit einem schnellerem Bin16Dez noch etwas Laufzeit zu gewinnen.
Zu meiner Überraschung musste ich aber feststellen, dass die Berechnung von 4960! mit dem etwas schnelleren Algorithmus von El Tangas[8] etwa genau so schnell ist, wie mit dem von mir optimierten Algorithmus von Douglas W. Jones.
Nun, das liegt daran, dass diese Routine im Vergleich zum 16-bit-MOD/DIV10 sehr viel seltener aufgerufen wird, nämlich bei 4960! nur 4959 mal.
D. h. bei ca. 2 µsec Laufzeitunterschied der beiden Algorithmen macht das insgesamt halt nur 10 msec aus, die bei meiner Stoppuhr-Messung (per "Alarm & Uhr" von WIN10) untergehen.
5000! mit Delphi auf dem PC (25.1.2021)
Schließlich hatte ich die kombinierte Binär/Dezimal-Methode doch noch in meinem Delphi-Programm implementiert und bei dieser Gelegenheit auf 5000! aufgebohrt (und damit auch die Summen der bearbeiteten Teilprodukt-Stellen ermittelt).
Die Rechenzeit für 192! lässt sich beim Delphi-Programm @3,3 GHz jedoch nicht mehr in msec messen, lediglich für 760! sind es gerade einmal 5 msec, für 1000! sind es dann schon 10 msec, also immerhin eine Steigerung um den Faktor 64 gegenüber der reinen Dezimal-Methode (mit ursprünglich vier Produkttermen).
333 @3,3
Für die Berechnung von 5000! benötigt mein steinaltes Delphi 5[11] nur 333 msec @3,3 GHz.
Das ist eben der Vorteil einer CPU mit 32/64-bit-Arithmetik gegenüber einer 8-bit-ALU beim kleinen AVR-µController (immerhin mit einem schnellen Multiplikationsbefehl, der in den vorgestellten Programmen vielfach verwendet wird).
Jetzt ist aber genug der Fakultäterei!
[1] Bei 2000! ist die stellenweise Summe der vier Teilprodukte nie größer als 39, bei 100! nie größer als 19 und bei 10! sogar nie größer als 8.
Lediglich beim Multiplizieren von Ziffern <>0 und <>1 und anschließendem Addieren des Carrys gibt es etwas größere Ergebnisse, allerdings (mindestens) bis 2000! (und das erst ab 59!) nie größer als 89 (von 9*9 + 8), so dass ein 8-bit-Register sowohl zum Multiplizieren mit Carry, zum Aufaddieren der Teilprodukte als auch für MOD_DIV10 allemal ausreicht.
[2] Zur Ansteuerung wird eine modifizierte TM1638-Library verwendet.
[3] Bei MIPS und anderen CPUs gibt es ein festverdrahtetes 0-Register (bei MIPS ist es R0).
[4] Wenn ich mich nicht verzählt habe, gibt es bei der Berechnung von 1000! trotz der Abfragen von zd[j] und fakul[k] auf Werte < 2 immer noch 2177871 reine Multiplikationen. Durch die Berechnung von MOD10 und DIV10 bei den Summenbildungen kommt ein Vielfaches davon dazu, so dass es insgesamt mehr als 10 Millionen Multiplikationen sein dürften.
[5] Der wissenschaftliche Windows-Rechner kann immerhin bis zu 3248! = 1,9736342530860425312047080034031e+9997 berechnen, allerdings nur in Exponentialdarstellung mit 32-stelliger Mantisse.
Beim wissenschaftlichen iPhone-Rechner ist bereits bei 103! = 9,90290071649e163 das Maximum erreicht und bei wissenschaftlichen Rechnern mit 8-stelliger Mantisse ist es meist nur 69! = 1,7112245e98.
[6] Genau genommen gibt es noch einen ATmega256RFR2 im VQFN-64-Gehäuse, der sogar 32 kByte SRAM (und einen 2,4-GHz-Transceiver) integriert hat. Ein solches Gehäuse ist für Hobbyisten kaum brauchbar, wenn es nicht bereits auf einer Platine verlötet ist.
[7] https://www.geeksforgeeks.org/factorial-large-number/
[8] Mit einigen ziemlich ausgefeilten Assembler-Tricks lässt sich die bereits sehr kurze Konvertierungszeit nahezu halbieren und damit die Ausführungszeit der Fakultäts-Berechnung entsprechend steigern, siehe umfangreiche Diskussion hier:
https://www.avrfreaks.net/forum/fast-conversion-integer-bcd-assembly-atmega328p
Aus Gründen der Übersichtlichkeit will ich es beim (optimierten) Algorithmus von Douglas W. Jones belassen.
[9] Die Addition von 6 ist ohne weitere Abfrage des Wertes von AKKU zulässig, da AKKU bei einem Carry der vorausgegangenen Addition von PLO ausreichend klein ist.
[10] Allerdings muss man dann die betroffenen oberen Ziffern vor der Ausgabe in inzwischen freigewordene Register retten, da diese sonst bei der Ausgabe durch Unterprogrammaufrufe überschrieben werden. Die Berechnung von 5014! klappt bei meinem Programm auch ohne diese "Rettungsaktion".
[11] Ein topaktuelles Delphi 10 benötigt mit exakt demselben, unveränderten Delphi5-Programm (das hat mich überrascht) immerhin 437 msec, ist also 1,3-mal langsamer. Und das von Delphi 10 erzeugte EXE-Programm ist nahezu 6-fach größer!