© Eberhard Haug 2003-2024
Optimale Darstellung dieser Website
bei aktiviertem
"Active Scripting"
(LED-Menü-Buttons)
Ackermann macht’s möglich (28.1.2019)
Die Ackermann-Funktion[1] (AF) ist eine stark rekursive Funktion und wird deshalb häufig für CPU-Tests bezüglich Verwendung des Arbeitsspeichers (insbesondere des Stacks) und der benötigten Ausführungszeit herangezogen.
Deshalb soll die AF nach einigen Vorbemerkungen auch hier (neben ein paar weiteren Programmen) verwendet werden, um die Leistungsfähigkeit von s’AVR auf den 8-bit-AVR zu überprüfen.
Auf eine Erklärung der mathematischen Hintergründe möchte ich an dieser Stelle verzichten, denn hierzu gibt es unendlich viele Abhandlungen in Büchern, Skripten und im WWW.
Hier eine Sprungtabelle für schnellen Zugriff:
JMP Auf vielen CPUs (28.1.2019)
JMP Meine Windows-Referenz (28.1.2019)
JMP Eine Übersicht (AF-Werte, 28.1.2019)
JMP Auf die Plätze ... (Ergebnisse, 28.1.2019)
JMP Quellprogramme (28.1.2019)
JMP Stack-Bedarf (18.9./8.10.2019, 28.2.2020)
JMP AF(3, 10) - geht doch! (3.10.2019)
JMP Leicht getunt: 2/7 : 5/9 : 4/9 (8.10.2019)
Auf vielen CPUs
Da mich die AF schon immer fasziniert hat seit ich mit Computern, µProzessoren und µControllern zu tun habe, hatte ich früh damit angefangen, die AF selbst zu programmieren - natürlich immer mit dem Bestreben, ein möglichst schnelles Programm für eine bestimmte CPU zu schreiben bzw. um verschiedene CPUs und verschiedene Programmiersprachen vergleichen zu können.
Anfangs waren es die CPUs Z80 und 68000, mit denen ich beruflich zu tun hatte. Ein ebenso µP/µC-infizierter Freund hatte zur gleichen Zeit die AF mit meinem Assemblerprogramm-Vorschlag auf seinem kleinen MC6802-System getestet - mit einer interessanten Feststellung (wie wir weiter unten noch sehen werden).
Schnell kamen weitere CPUs bzw. Rechner dazu, die ich "beackert" hatte.
Da der CPU-Takt natürlich nicht immer derselbe war, habe ich schließlich die Ausführungszeit der AF für einen sinnvollen Vergleich auf eine einheitliche Größe umgerechnet und einen Ackermann-Index (AI) eingeführt, der praktischerweise wie folgt definiert ist:
AI = (Ausführungszeit/msec * CPU-Frequenz/MHz) / AF(x, y)
Die "Maßeinheit" des Ackermann-Index ist eigentlich msec * MHz, genaugenommen aber dimensionslos, da die Ausführungszeit auf die CPU-Zykluszeit bezogen ist.
Die Division durch AF(x, y) hält den Index in Grenzen[4].
Zum Vergleichen verschiedener CPUs/Rechner, Programmiersprachen und Betriebssysteme muss man also immer dieselben Parameter x und y von AF(x, y) verwenden und sinnvollerweise neben der Ausführungszeit auch den CPU-Takt, die Speicherausstattung, etc. erfassen. Der daraus bestimmte AI ist dann eine ziemlich gute Vergleichsaussage, wobei jeweils der kleinere Wert gewinnt.
Ende 1999 hatte ich damit angefangen, mit dem inzwischen steinalten Delphi-5 (mit dem auch s’AVR erstellt ist, was aber kein Nachteil sein muss) in Pascal ein Windows-Programm zuschreiben, das nicht nur die AF rekursiv berechnet (das ist eine leichte Übung), sondern bei Bedarf auch die Rekursionstiefe grafisch darstellt, so dass man eine Vorstellung davon hat, was im Stack des CPU-Systems so vor sich geht.
Da die Grafikausgabe sehr zeitintensiv ist, muss man sie zur Bestimmung der tatsächlichen Ausführungszeit der AF natürlich abschalten! Mit Grafik heißt es deshalb auch "Zeichenzeit" statt "Rechenzeit".
Im Laufe der Zeit sind noch einige Extras dazugekommen, wie z.B. die Ausgabe der Anzahl der Funktionsaufrufe und der maximalen Rekursionstiefe, die ein Hinweis auf den Stack-Bedarf ist.
Und so schaut das Ergebnis einer Berechnung von AF(3, 8) mit Grafikausgabe aktuell auf meinem Windows-10-PC (mit i5-CPU) aus:
Man könnte sich die vom Programm ausgegebene Grafik[2] im unteren (größeren) Bereich des Programm-Fensters beim gezeigten Beispiel als 3D-Vorhang vorstellen, der bei größeren AF-Parametern langsam zugezogen wird (und je nach AF-Parameter auch sehr unterschiedlich ausschaut).
Auf dem Programmfenster steht auch gleich die Definition der Ackermann-Funktion.
Und statt stolzen 58 sec Zeichenzeit wären es ohne Grafikausgabe bei AF(3, 8) nur noch 15 msec Rechenzeit (bei vollständig rekursiver Berechnung)!
Bei sehr kleinen AF-Parametern sind es eher bunte und schnell (hier < 1 sec) wachsende Eiszapfen in 2D:
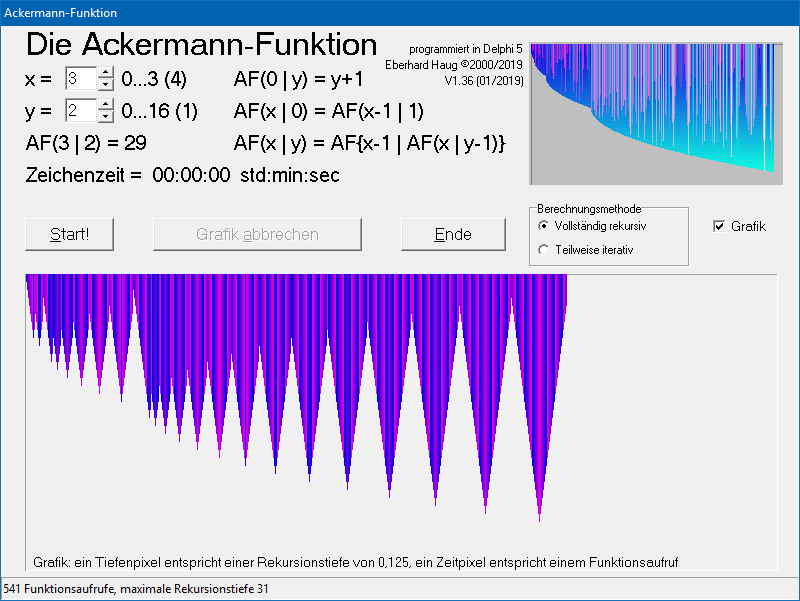
Bei diesem Beispiel sieht man sehr schön das stetige Ab-und-Auf im Stack, bis schließlich nach Erreichen der maximalen Stack-Tiefe das Ergebnis am Ende des letzten Aufstiegs zur Verfügung steht (das aber nicht in der Grafik erkennbar ist, sondern separat als AF(3|2) = 29 ausgegeben wird).
Mit den angegebenen Pixeleinheiten könnte man bei diesem Beispiel sogar die Zahl der Funktionsaufrufe und die Rekursionstiefe aus der Grafik ablesen, wenn auch etwas mühsam. Deshalb werden diese Werte inzwischen vom Programm gezählt und unten in der Statuszeile ausgegeben.
Damit der interessierte Leser eigene AF-Untersuchungen anstellen kann (so er einen schnellen PC oder viel Zeit hat), stelle ich mein Windows-Programm bei Bedarf gerne zur Verfügung.
Bevor es ans Eingemachte geht, zunächst ganz unabhängig von jeglicher CPU und Programmiersprache eine Tabelle mit diversen AF-Ergebnissen von zweckmäßigen Parametern x und y, der Anzahl der zugehörigen Funktionsaufrufe und der maximalen Rekursionstiefe (also dem letzten Peak vor dem AF-Ergebnis), jeweils für die vollständig rekursive Berechnung:
Die Anzahl der Funktionsaufrufe[5] und der maximalen Rekursionstiefe dieser Tabelle wurden vom Programm gefunden und in die Tabelle übertragen.
Nach (sehr) langem Suchen habe ich auch eine ziemlich komplexe Formel zur Berechnung der Anzahl der Funktionsaufrufe für AF(3, y) und deren clevere Herleitung[3] gefunden:
Anzahl der AF(3, y)-Funktionsaufrufe = (128 * 4^y − 120 * 2^y + 9*y + 37)/3
Eine Verifizierung mit dieser Formel bestätigt exakt die vom Programm gefundenen Werte (immerhin)!
Ein Versuch, diese Formel direkt aus den Tabellenwerten herzuleiten, kann nur scheitern.
Noch eine Formel (18.9.2019)
Inzwischen bin ich für AF(3, y) über eine weitere Formel[7] jüngeren Datums gestolpert, die aber auf eine Umformung der obigen hinausläuft und natürlich dasselbe (korrekte) Ergebnis liefert:
Anzahl der AF(3, y)-Funktionsaufrufe = 128 * (4^y - 1)/3 - 40 * (2^y - 1) + 3*y + 15
Die oft (teilweise mit Tippfehlern) zitierte Formel gemäß Yngve Sundblad (1971):
Anzahl der AF(3, y)-Funktionsaufrufe ≠ AF(3, y) + 12^y - 2
ist dagegen definitiv nicht korrekt. Daher habe ich in dieser Formel das Ungleichheitszeichen verwendet.
Werte für die Anzahl der Funktionsaufrufe bis AF(3, 3) nach der Sundblad-Formel sind kleiner, darüber sind sie schnell wachsend größer. Es wundert mich sehr, dass die Ergebnisse nicht wenigstens für AF(3, 0) und AF(3, 1) überprüft wurden. Deshalb kann es sich nur um ein Missverständnis handeln.
Und was ist mit AF(4, y)?
AF(4, 0) = 13 ist trivial und AF(4, 1) = 65533 lässt sich genau so gut und schnell berechnen wie AF(3, 13). Die Rekursionstiefe ist allerdings um 1 größer, siehe Tabelle.
Von AF(4, 2) und darüber lässt man am Besten die Finger, denn das Ergebnis von AF(4, 2) ist 2^65536 - 3 und die Rekursionstiefe ist 2^65536. Das ist eine Zahl mit 19729 Stellen ...
Auf die Plätze ... (28.1.2019)
Nach der langen Vorrede sollen nun selbst ermittelte Zahlenwerte sprechen, die über die Jahre mehr oder weniger vollständig gesammelt und in einer umfangreichen Tabelle zusammengefasst wurden.
Ein Auszug mit den wichtigsten Spalten soll hier gezeigt werden:
Der Sieger aus jeder AF(3, y)-Gruppe ist jeweils grün markiert, die Nächstplatzierten orange.
Gelbe Werte waren mit der Armbanduhr "geschätzt" und wurden für den 6802 durch den codekompatiblen 68HC11 neuerdings per Scope genauer gemessen (genau genommen sollte sich für beide derselbe AI ergeben).
Erkenntnisse
- 6802/68HC11 waren in meiner Liste lange die AF-Sieger bis die RISC-Prozessoren von MIPS auf den Markt kamen [siehe AF(3, 9) und AF(3, 10)], sind aber trotz CISC-Architektur je nach AF-Parameter auch heute immer noch auf den vorderen Rängen mit dabei.
- Die 8-Bit-AVR können bei der AF absolut mit großen RISC-CPUs mithalten, wobei modernere Compiler für letztere vermutlich bessere Ergebnisse zeigen als der Code meines alten Delphi-5, der aber angeblich schneller ist, als Code neuerer Delphi-Versionen.
Vielleicht kann das jemand von meinen Lesern durch eigene Untersuchungen bestätigen? - Im Vergleich zu Arduino C (kompiliert mit Arduino-Tools) und avr gcc (kompiliert mit Atmel Studio) zeigt s’AVR auf denselben AVR-CPUs deutlich bessere Ergebnisse, siehe AF(3, 5) und AF(3, 6).
- Bis einschließlich AF(3, 10) sind die 8-bit-AVR-CPUs in Kombination mit s’AVR schneller als andere von mir untersuchte CPUs und Programmiersprachen.
Ich bin gespannt auf Kommentare und freue mich über AF-Ergebnisse (auch mit anderen CPUs) meiner Leser.
Quellprogramme (28.1.2019)
Zur Diskussion der Ergebnisse oder für eigene Untersuchungen durch meine Leser möchte ich nachfolgend den von mir verwendeten Quellcode zur Verfügung stellen.
Mein Delphi-Programm setzt die oben gezeigten AF-Definitionen direkt in Pascal um:
function AF(x,y: longword): longword; register; // no extras, full speed!
begin
if x = 0 then af := y+1
else if y = 0 then af := af(x-1, 1)
else af := af(x-1, af(x,y-1));
end;
Die Rechenzeit wird mittels Differenz der Windows-Systemvariablen "now" vor und nach dem AF-Aufruf bestimmt.
Für Arduino lautet die AF-Routine in C wie folgt:
int ackermann(byte m, int n) // m can be byte (short n would be same as int n)
{
if (!m) return n + 1;
if (!n) return ackermann(m - 1, 1);
return ackermann(m - 1, ackermann(m, n - 1));
}
Für eine genaue Messung der Rechenzeit per Scope mit einem ATmega328 wird an LED13 ein Trigger-Signal ausgegeben und die AF(3, 6) [mehr lässt der Stack nicht zu] in einer Endlosschleife ausgeführt:
void loop()
{
byte m; int n;
digitalWrite(led13, LOW);
ackermann(3, 6);
digitalWrite(led13, HIGH);
delay(1); // 1 ms
}
Hier der vollständige C-Code aus Atmel Studio (wobei ich bei den Ergebnissen keinen Unterschied zwischen GCC und GPP feststellen konnte):
#define F_CPU 16000000UL // 16 MHz
#include <avr/io.h>
#include <util/delay.h>
#define LED_ON PORTB |= (1 << PORTB5)
#define LED_OFF PORTB &= ~(1 << PORTB5)
#define LED_TOGGLE PINB |= (1 << PINB5)
int ackermann(uint_fast8_t m, int n)
{
if (!m) return n + 1;
if (!n) return ackermann(m - 1, 1);
return ackermann(m - 1, ackermann(m, n - 1));
}
int main(void)
{
DDRB |= (1 << DDB5); // Port B, Bit 5 is output
while(1)
{
LED_OFF;
ackermann(3, 6); // AF(3, 6)
LED_ON;
_delay_ms(1); // short HIGH pulse for the scope (1 ms)
}
}
Und per s’AVR wird die eigentliche AF-Routine kaum aufwendiger, nämlich ebenso mit nur zwei einfachen IF-Abfragen:
AF: ; Ackermann function AF(x, y)
; where x = xl = R26, y = yh:yl = R29:R28, result in yh:yl
IF xl == #0 ; check x ? 0
adiw y,1 ; AF(0, y) = y + 1
ret ; the only and final return within AF
ENDI
adiw y,0 ; to check y ? 0
IF NZ ; testing for y <> 0 (NZ) first speeds up for larger y values
sbiw y,1 ; y := y - 1
push xl
rcall AF ; recursive call AF(x, y-1), result in yh:yl
pop xl
subi xl,1 ; x := x - 1
rjmp AF ; recursive call,
; same as rcall AF(x-1, AF(x, y-1)) | ret (tail call)
ENDI ; all other cases must be AF(x, 0) = AF(x-1, 1)
subi xl,1 ; x := x - 1
ldi yl,1 ; y := 1 (additional clr yh is not required
; as yh:yl was zero before)
rjmp AF ; recursive call, same as rcall AF(x-1, 1) | ret (tail call)
Zum genauen Messen der Rechenzeit wird ebenfalls ein Trigger-Signal in einer Endlosschleife verwendet (hier mit 100 ms Verzögerung zum Messen längerer Rechenzeiten für AF(3, 9) mit dem ATmega1284, der 16 kByte SRAM für den Stack zur Verfügung hat):
LOOP ; loop AF to measure the time by scope
mov xl,AFX ; get AF parameter X
mov yl,AFYL ; get AF parameter YL
mov yh,AFYH ; get AF parameter YH
cbi PORTC,0 ; pin off, trigger scope on falling edge
rcall AF
sbi PORTC,0 ; pin on, measure time on rising edge
rcall delay100ms
ENDL
Die in diesem AF-Code verwendeten Tail-Calls sind ein gängiger Assembler-Optimierungstrick, der auch von den genannten C-Compilern verwendet wird.
Die C-Compiler verwenden noch ein paar weitere Tricks. So wird bei Register R1 immer der Inhalt 0 vorausgesetzt und von beiden C-Compilern verwendet (nicht so von s’AVR).
Dennoch ist der von s’AVR erzeugte Code mit 30 Bytes deutlich kompakter (und entsprechend schneller) als jener der C-Compiler, die 48 Bytes (Arduino C) bzw. 56 Bytes (avr gcc) für die eigentliche AF-Routine benötigen.
Die von den C-Compilern erzeugten Assembler-Listings auf Anhieb zu verstehen, ist allerdings schon eine Herausforderung ...
Interessant ist vielleicht noch, dass 6802/68HC11 (8-bit-CISC-CPUs) nur 22 Bytes Programmspeicher und der MK68200 (16-bit-CISC-CPU) bereits 36 Bytes für den AF-Code in Assembler-Sprache benötigen.
Stack-Bedarf (18.9./8.10.2019)
Um insbesondere für µC mit wenig RAM bzw. Stack abschätzen zu können, für welche AF-Parameter eine vollständig rekursive AF-Berechnung überhaupt erfolgreich sein kann, lässt sich der Stack-Bedarf für den ungünstigsten Fall ("Worst-Case") sehr einfach über die maximale Rekursionstiefe bestimmen.
Bei meinem s’AVR-Programm sind es nach dem ersten rcall AF ohne PUSH (innerhalb der LOOP-Schleife) diese beiden Befehle, die den Stack belasten:
push xl
rcall AF ; recursive call AF(x, y-1), result in yh:yl
Beim Push-Befehl wird ein 8-Bit-Register auf den Stack geschrieben, wodurch ein Byte belegt wird.
Beim RCALL-Befehl wird die Rücksprungadresse auf den Stack geschrieben, wodurch entweder zwei Bytes belegt werden (bei allen AVR mit 16-Bit-Befehlszähler, was die Mehrzahl ist) bzw. drei Bytes bei AVR mit 22-Bit-Befehlszähler (nur ATmega2560/2561 und einige ATxmega), die aber alle nur maximal 8192 Bytes SRAM haben und deshalb bei meinen Untersuchungen außen vor bleiben.
Der Stack-Bedarf für das vorgestellte s’AVR-basierende AF-Programm beträgt bei allen AVR mit 16-Bit-Befehlszähler also Worst-Case:
Stack-Bedarf/Byte = 3 * maximale Rekursionstiefe - 1
Sprich, für AF(3, 9) benötigt ein ATmega1284 insgesamt höchstens 12275 Bytes von maximal 16384 Bytes Stack. Es ist also noch reichlich SRAM übrig (nach Berechnen der AF sowieso).
Die ATmega2560/2561 könnten wegen 8192 Bytes verfügbarem internem[6] SRAM dagegen nur maximal AF(3, 8) berechnen, wofür 8175 Bytes Stack nötig wären. Bestenfalls wären also 17 Bytes SRAM übrig.
Ein ATmega328P "schafft" wegen 2048 Bytes SRAM nur maximal AF(3, 6). Es bleiben aber noch mindestens 525 Bytes SRAM frei.
Für andere µC lässt sich der Stack-Bedarf für die vollständig rekursive Ackermann-Funktion sinngemäß aus den jeweils für den AF-Aufruf verwendeten Assembler-Befehlen bestimmen.
Den Stack im Detail betrachtet (28.2.2020)
Aufgrund der Tail-Calls ist der tatsächliche Stack-Bedarf beim s’AVR-Programm ganz offensichtlich kleiner als über die maximale Rekursionstiefe obiger Tabelle berechnet, da an diesen Stellen sowohl der RCALL-Befehl mit seinem Stack-Bedarf entfällt, als auch der PUSH-XL-Befehl (um sonst den x-Wert zu retten).
Aber auch ohne Tail-Call entfällt an diesen beiden Stellen immer der PUSH-Befehl.
Um den Unterschied herauszufinden, habe ich bei jedem AF-Aufruf per Programm den Stack-Pointer immer direkt nach dem AF-Aufruf betrachtet und den minimalen Wert festgehalten, um so den tatsächlichen Stack-Bedarf der unterschiedlichen AF-Programme zu bestimmen.
Das Ergebnis ist ernüchternd, denn die Tail-Calls sparen am Stack-Bedarf gegenüber den Worst-Case-Formeln bei AF(3, y) unabhängig von y nur 9 Bytes bei Standard-Aufrufen und 6 Bytes bei kurzen Aufrufen (letztere insbesondere für bis zu AF(3, 10) mit dem ATmega1284, siehe weiter unten).
Mit anderen Worten: Bei AF(3, 10) bleiben beim ATmega1284 mit einem kurzen AF-Aufruf (zwangsläufig) und Tail-Calls noch genau 9 Stack-Bytes[9] frei.
Ohne Tail-Calls werden durch die fehlenden PUSH-Befehle an diesen Stellen unabhängig von den Aufrufmethoden (rcall bzw. scall) und unabhängig von Parameter y gegenüber den Worst-Case-Formeln generell nur 3 Bytes am Stack eingespart.
Unabhängig vom Stack-Bedarf sparen die Tail-Calls und die fehlenden PUSH-Befehle dennoch viel Rechenzeit (und etwas Programmspeicher).
AF(3, 10) - geht doch! (3.10.2019)
Es hat mich ziemlich gewurmt, dass mit dem ATmega1284 bei AF(3, 9) immer noch 1/4 des Stack frei ist, aber halt viel zu wenig, um AF(3, 10) vollständig rekursiv berechnen zu können.
Nach der Analyse des Stack-Bedarfs kam mir die Idee, statt dem AF-Aufruf per rcall, der zwei Stack-Bytes benötigt, einen modifizierten "kurzen" AF-Aufruf zu verwenden, der den Stack jeweils nur mit einem Byte belastet, womit sich der Stack-Bedarf dann im Worst-Case wie folgt berechnet:
Stack-BedarfShort/Byte = 2 * maximale Rekursionstiefe - 1
Voraussetzung hierfür ist, dass sich der AF-Aufruf und das AF-Unterprogramm im selben 256-Byte-Programmspeicher-Segment befinden, so dass man für den Rücksprung nur das Low-Byte im Stack speichern muss. Diese Bedingung ist beim s’AVR-Ackermann-Programm leicht zu erfüllen.
Und die nötigen Befehlszeilen sind ebenso einfach.
Da man keinen direkten Zugriff auf den AVR-Befehlszähler hat, muss man sich mit dem Z-Register behelfen, mit dem man indirekte Sprünge ausführen kann (hier für die Rücksprünge[8] aus der rekursiv aufgerufenen Ackermann-Funktion).
Und so schaut das Macro scall für einen kurzen AF-Aufruf aus, wobei bei dieser Variante sowohl die Adresse des Unterprogramms (hier AF) als auch die Rücksprungadresse (immer direkt nach dem Aufruf) als Macro-Parameter angegeben werden müssen:
.MACRO scall ; Macro to call a subroutine using only one byte on the stack
; usage: scall SubroutineAddress, ReturnAddress
; ZH:ZL are used for the return address, where
; ZH permanently keeps the high byte of the return address,
; ZL is loaded with the low byte of the return address
ldi ZL,low(@1)
push ZL
rjmp @0 ; rjmp instead of rcall
; local returning is done by "pop ZL" and "ijmp"
.ENDMACRO
Register ZH wird im Hauptprogramm während der Initialisierungsphase mit dem High-Byte der Adresse des AF-Unterprogramms geladen und man sorgt dafür, dass das AF-Unterprogramm und die Rücksprungadressen (= Adresse des oder der AF-Aufrufe) z. B. immer im Bereich $0100 bis $01ff liegen, indem man den Programmbeginn bei $0100 legt (Adressen ggf. in der LSS-Datei überprüfen).
Nur ein Macro-Parameter (27.2.2020)
Man kann das scall-Macro auch mit nur einem Parameter schreiben und ZL PC-relativ laden:
.MACRO scall ; Macro to call a subroutine using only one byte on the stack
; usage: scall SubroutineAddress
; ZH:ZL are used for the return address, where
; ZH permanently keeps the high byte of the return address,
; ZL is loaded with the low byte of the return address
ldi ZL,low(PC+3) ; return address after rjmp
push ZL
rjmp @0 ; rjmp instead of rcall
; local returning is done by "pop ZL" and "ijmp"
.ENDMACRO
Der Aufruf der Ackermann-Funktion mit nur einem Macro-Parameter heißt dann schlicht:
scall AF ; macro to call AF using only one byte on the stack
ZH muss natürlich weiterhin vor dem ersten Aufruf im Hauptprogramm geladen werden.
Der kurze Rücksprung
Damit das Programm beim Rücksprung direkt nach dem Aufruf des Unterprogramms fortgesetzt wird, muss man (wie im scall-Macro vermerkt) das ursprüngliche ret durch folgende Befehlsfolge ersetzen (die genau so schnell ist, nur ein Befehlswort mehr benötigt):
pop ZL ; modified return after scall AF
ijmp ; return via indirect call and ZH:ZL
Oder man definiert ein einfaches Macro sret mit genau dieser Befehlsfolge:
.MACRO sret
pop ZL ; modified return after scall AF
ijmp ; return via indirect call and ZH:ZL
.ENDMACRO
Die modifizierte AF-Routine mit kurzem AF-Aufruf (ein Macro-Parameter) und modifiziertem Return (jeweils rot markiert) schaut damit schließlich so aus:
AF: ; Ackermann function AF(x, y)
; where x = xl = R26, y = yh:yl = R29:R28, result in yh:yl
IF xl == #0 ; check x ? 0
adiw y,1 ; AF(0, y) = y+1
; ret ; the only and final return within AF
sret ; modified return (macro) after scall AF
ENDI
adiw y,0 ; to check y ? 0
IF NZ ; testing for y <> 0 (NZ) first speeds up for larger y values
sbiw y,1 ; y := y - 1
push xl
;rcall AF ; recursive call AF(x, y-1), result in yh:yl
scall AF ; macro to call AF using only one byte on the stack
pop xl
subi xl,1 ; x := x - 1
rjmp AF ; recursive call,
; same as rcall AF(x-1, AF(x, y-1)) | ret (tail call)
ENDI ; all other cases must be AF(x, 0) = AF(x-1, 1)
subi xl,1 ; x := x - 1
ldi yl,1 ; y := 1 (additional clr yh is not required
; as yh:yl was zero before)
rjmp AF ; recursive call, same as rcall AF(x-1, 1) | ret (tail call)
Mit dieser trickreichen Methode werden im Vergleich zum Original pro Aufruf und Rückkehr nur drei zusätzliche Programmspeicher-Worte mit nur zwei zusätzlichen Speicherzyklen benötigt.
Dadurch wird AF(3, 9) zwar etwa 10% langsamer, aber es lässt sich jetzt auch AF(3, 10) mit dem ATmega1284 vollständig rekursiv berechnen (in ca. 34,8 sec @18 MHz).
Und der ATmega1284 hat damit im Vergleich zu den anderen getesteten CPUs immer noch den besten Ackermann-Index, nämlich 38,2 bei AF(3, 9) und 76 bei AF(3, 10)!
Mit derselben Methode könnte ein ATmega328 nun auch AF(3, 7) berechnen und bliebe per s’AVR mit einem Ackermann-Index von 9,5 (im Vergleich zu 8,8 mit einem ATmega1284 und der originalen AF) weiterhin mit an der Spitze.
Leicht getunt: 2/7 : 5/9 : 4/9 (8.10.2019)
Diese Überschrift ist keine Zauberformel, sondern es sind die Verhältnisse von Programmspeicherworten und Taktzyklen von AF-Aufrufen und Rücksprüngen nach der Originalversion per rcall mit Wort-Adresse, per Macro scall mit Byte-Adresse und einer weiteren (einfacheren) Variante per rcall und nachträglich im Stack verkürzter Wort-Adresse.
Letzteres wird erreicht, indem man nach dem Aufruf per rcall mit dem ersten Befehl der AF-Routine das MSByte der Rücksprungadresse (das als letzter Stack-Eintrag steht!) wieder per pop ZH vom Stack entfernt (damit dort der gewünschte Speicherplatz frei wird) und damit für das spätere ijmp gleich in ZH ablegt, wodurch der Rücksprung nur dann korrekt zur aufrufenden Stelle erfolgt, wenn der AF-Aufruf und die AF-Routine im selben 256-Byte-Programmspeicher-Segment liegen (wie bei der Methode scall).
ZH muss bei dieser Methode also nicht mehr in der Initialisierungsphase mit dem High-Byte der Adresse des AF-Unterprogramms geladen werden.
Der Rücksprung erfolgt wie bei scall ebenfalls per Macro sret, das heißt, das LSByte der Rücksprungadresse wird vom Stack in das Register ZL geholt und schließlich per ijmp und Doppelregister ZH:ZL indirekt zur jeweiligen Aufrufstelle zurückgesprungen.
Abgesehen von der einfacheren (besser überschaubaren) Methode im Vergleich zu scall gibt es innerhalb der AF-Routine den Gewinn von einem Programmspeicherwort, aber leider keinen Laufzeitgewinn - 4/9 eben.
Damit das dann auch wie gewünscht klappt, dürfen die Tail-Calls (per rjmp) innerhalb der AF-Routine nicht an den Anfang der AF-Routine erfolgen, sondern direkt nach dem Befehl pop ZH (sonst gerät der Stack durcheinander).
Im Klartext (23.10.2019)
Statt vielen Worten hier die getunte Version auch noch als s’AVR-Quellprogramm (immer noch vollständig rekursiv), wohlgemerkt speziell für AF(3, 10) auf einem ATmega1284 oder für AF(3, 7) auf einem ATmega328:
AF: ; Ackermann function AF(x, y)
; where x = xl = R26, y = yh:yl = R29:R28, result in yh:yl
pop zh ; take high byte of the return address from stack to zh,
; which saves plenty of stack for AF(3, 10) on ATmega1284
AFs:
IF xl == #0 ; check x ? 0
adiw y,1 ; AF(0, y) = y+1
; ret ; the only and final return within AF
sret ; modified return (macro) after rcall AF, pop ZH
ENDI
adiw y,0 ; to check y ? 0
IF NZ ; testing for y <> 0 (NZ) first speeds up for larger y values
sbiw y,1 ; y := y - 1
push xl
rcall AF ; recursive call AF(x, y-1), result in yh:yl
pop xl
subi xl,1 ; x := x - 1
;rjmp AF ; recursive call,
; same as rcall AF(x-1, AF(x, y-1)) | ret (tail call)
rjmp AFs ; recursive tail call, modified
ENDI ; all other cases must be AF(x, 0) = AF(x-1, 1)
subi xl,1 ; x := x - 1
ldi yl,1 ; y := 1 (additional clr yh is not required
; as yh:yl was zero before)
;rjmp AF ; recursive call, same as rcall AF(x-1, 1) | ret (tail call)
rjmp AFs ; recursive tail call, modified
Natürlich klappen damit auch kleinere AF(x, y) - halt entsprechend langsamer, aber immer noch schneller als die Konkurrenz.
Fazit (28.1.2019)
s’AVR erzeugt sehr effektiven und schnellen Programm-Code und muss einen Vergleich mit AVR-C-Compilern nicht scheuen - gute AVR-Assembler-Kenntnisse beim Schreiben der s’AVR-Programme vorausgesetzt.
Mit ein paar Programmiertricks lässt sich sogar AF(3, 10) vollständig rekursiv und ziemlich flott per ATmega1284 und seinem internen SRAM berechnen.
Die Ackermann-Funktion ist zwar eine sehr einfache (wenn auch rechenintensive) Funktion, ich erwarte bei komplexeren AVR-Programmen unter Verwendung von s’AVR aber eine ähnlich gute Effizienz im Vergleich mit AVR-C-Compilern.
[1] Genau genommen ist hier eine vereinfachte Variante genannt Ackermann-Péter-Funktion (1935) gemeint, die 1948 von Raphael Robinson noch weiter vereinfacht wurde und die (etwas umformuliert) schließlich zur "modernen" Ackermann-Funktion geführt hat.
[2] Die Grafik von AF(3,8) ist Bestandteil des Programmfensters rechts oben. Sie wurde allerdings auf einem älteren Bildschirm mit anderer Auflösung erstellt.
[3] Diese Studie ist ursprünglich vom April 1975 (!):
https://www.researchgate.net/publication/226959069_Ackermann%27s_function
An weiteren Stellen im WWW finden sich andere Formeln für die Anzahl der Funktionsaufrufe der Ackermann-Funktion (teilweise auch mit Tippfehlern von anderen Quellen übernommen), die stark abweichende Werte ergeben, als jene von B. A. Wichmann und von mir gefundene.
Auch bezüglich der maximalen Rekursionstiefe (siehe obige Tabelle) gibt es widersprüchliche Aussagen.
Offensichtlich ist sie bei AF(3,y) um zwei größer als AF(3,y) und bei AF(4,y) ist sie um drei größer als AF(4,y).
[4] Mit einem zusätzlichen Faktor 2^(10-y) würde der Index für alle AF(3, y) überwiegend konstant bleiben.
[5] Mit Unterstrich statt Tausenderpunkt (oder Leerzeichen), damit (manche) Browser keine Telefonnummern oder IP-Adressen daraus machen.
[6] Mit externem SRAM könnten die ATmega2560/2561 zwar bis zu AF(3, 10) und die ATmega640/1280/1281 (und ein paar weitere Ausführungen mit externem SRAM) sogar bis zu AF(3, 11) berechnen, wären aber bei bis zu AF(3, 9) bezüglich Rechenzeit wegen den mindestens doppelt so langen externen SRAM-Zugriffen gegenüber ATmega1284 deutlich unterlegen (insbesondere die ATmega2560/2561 wegen deren 22-Bit-Befehlszähler).
[7] siehe:https://math.stackexchange.com/questions/2511594/ackermann-function-how-to-calculate-the-number-of-times-it-calls-itself
Peter Košinár gibt hier sowohl eine allgemein gültige Methode zur Bestimmung der Anzahl der AF-Aufrufe an, als auch die für AF(3, y) vereinfachte Form.
[8] Der ganze Aufwand ist nötig, da die Rücksprungadresse wegen genau einer Ausnahme nicht immer dieselbe ist, nämlich einmal ist es der Rücksprung ins Hauptprogramm (wenn die AF vollständig rekursiv abgearbeitet ist) und sonst ist es immer an die Stelle direkt nach dem Aufruf innerhalb der AF selbst.
[9] Im Assembler-Listing meines Ackermann-Programms für den MK68200 (ebenfalls mit Tail-Calls) habe ich notiert:
"AF(3, 10) keeps 18 bytes free in the total stack of 32 KB."
Damals (1984) hatte ich die Belegung des Stacks einfach mit einem Memory-Dump per Incircuit-Emulator bestimmt.