© Eberhard Haug 2003-2026
Optimale Darstellung dieser Website
bei aktiviertem
"Active Scripting"
(LED-Menü-Buttons)
In dieser Rubrik geht es um das Ziehen von Quadrat- und Kubik-Wurzeln per s’AVR und sogar von Hand mit einem 4-bit-Rechenwerk, aufgebaut mit historischen Bauelementen.
Der kurze Weg geht hier entlang:
- Die C-Wurzel (21.8.2021)
- Summierende Wurzel-Approximation (23.8.2021)
- Subtrahierende Wurzel-Approximation (ähnlich Toepler-Verfahren, 8.3.2023)
- Das Toepler-Verfahren auf einem 4-bit-Rechenwerk (20.3.2023)
- Die Turbo-Toepler-Wurzel (15.3.2023)
- Die Kubikwurzel (26.8.2021)
Schnell die (Quadrat-) Wurzel gezogen (3.8.2021)
SQRT16 - Schnell die (Quadrat-) Wurzel gezogen (3.8.2021)
Auf der Suche nach einer Quadratwurzel per AVR ist mir zunächst eine relativ schnelle Routine für die SX-Controller (von Scenix/Ubicom, später Parallax) in den Sinn gekommen. Da diese für meinen Precompiler SXp geschrieben war (aber ursprünglich nicht auf meinem Mist[2] gewachsen ist), wäre ein Umschreiben auf s’AVR nicht allzu schwierig geworden.
Leider ist das bei der SX-Routine angewandte Konzept nicht so einfach durchschaubar (mehrseitige Beschreibung des Verfahrens mit ausschließlich Bit-Setzen, Rotieren, Subtrahieren und Addieren), so dass ich noch etwas weiter zurückgeblickt habe, nämlich auf ein Assembler-Programm, das ich bereits 1985 für den sehr schönen 16-bit-CISC-µC MK68200[3] von Mostek geschrieben hatte.
Und damit wird das Wurzelziehen denkbar einfach und sogar deutlich schneller - sofern der verwendete µC einen Hardware-Multiplizierer hat bzw. Multiplizierbefehle unterstützt.
Da meine Programme meist auf den ATmegas laufen, war das natürlich kein Problem.
Sukzessive Approximation
Das Stichwort für das dabei angewandte Wurzelziehen heißt sukzessive Approximation, die u. a. auch für schnelle A/D-Wandler verwendet wird.
Um eine Wurzel einer 16-bit-Zahl ganzzahlig darzustellen, benötigt man wenigstens 8 Bit, genaugenommen sogar 9 Bit, falls der Radikand größer als 65.280 (0xFF00) ist, denn dann ist das Ergebnis bei korrektem Runden 256 (0x01FF).
Zunächst sollen aber 8 Bit für das Ergebnis genügen, da sich das 9. Bit erst beim Runden ergibt.
Erklärt mit wenigen Worten
Für die Wurzelberechnung tastet man sich durch versuchsweises Setzen von einzelnen Ergebnis-Bits (beginnend mit dem höchstwertigen), Quadrieren dieser damit gebildeten 8-bit-Zahl und Vergleichen mit dem Radikanden bitweise an die richtige Lösung heran: Ist das Quadrat zu groß, wird das jeweilige Bit zurückgenommen und das nächst niederwertigere Bit gesetzt. Passt das Ergebnis exakt, hat man bereits die Lösung und kann die Prozedur eigentlich mit diesem Ergebnis beenden. Sonst muss man weitere Bits setzen bzw. rücksetzen, bis das niederwertigste Bit erreicht ist.
Eine runde Sache
Spätestens nach bis zu 8 Versuchen hat man schon fast das korrekte Ergebnis. Es muss nur noch richtig (auf-) gerundet werden.
Für diese SQRT-Berechnungsmethode gibt es inzwischen zuhauf Vorschläge. Erstaunlicherweise wird das richtige Runden dabei meist unterschlagen.
Bestenfalls wird noch der ganzzahlige Rest zum Radikanden angegeben. Dieser Rest liegt im Bereich 0 ... 2*Quadratwurzel, kann unter Umständen also ganz schön groß sein.
Damit kann man vermuten, dass fast die Hälfte (nämlich 49,8%) aller Ergebnisse nicht korrekt gerundet ist.
Sofern man den ganzzahligen Rest hat, ist der Weg zur richtig gerundeten Lösung aber gar nicht mehr so weit, denn zieht man diesen vom gefundenen vorläufigen Ergebnis ab und das Ergebnis der Subtraktion ist negativ, dann muss man die Wurzel aufrunden, sprich inkrementieren. Ansonsten hat man bereits die richtig (ab-) gerundete Wurzel. So einfach ist das!
Übersichtlich
Und so schaut das kleine und feine SQRT16-Programm in strukturierter AVR-Assemblersprache s’AVR aus (mit vielen Kommentaren versehen, falls jemand tiefer einsteigen möchte):
; SQRT16:
; This subroutine calculates the rounded 9 bit integer square root y of a 16 bit value x:
; y = SQRT(x)
; (c) Eberhard Haug 03-AUG-2021
; Registers RADHI:RADLO = x are kept unmodified. RADHI:RADLO = XH:XL would be a good choice.
; But instead of XH:XL any other AVR registers (or register pairs) can be used.
; The correctly rounded 9 bit result y resides in YH:YL.
; YH is also used as bit position register until the 9th bit is required.
; Instead of YH and YL any other double registers can be used (which allow addiw).
; PHI:PLO = R1:R0 are used to calculate both the square and the integer remainder of the result
; (2's complement). In total only 6 AVR registers are used.
; Method being used: Successive approximation.
; SQRT16 can be expanded to SQRT24, SQRT32 etc.
SQRT16:
ldi YH, 0x80 ; start with MSB
clr YL ; clear result y (8 bits so far)
REPEAT
or YL, YH ; set next bit position
mul YL, YL ; result y^2 in PHI:PLO
sub PLO, RADLO ; subtracting needs same time as comparing, but simplifies rounding
sbc PHI, RADHI ; now PHI:PLO = y^2 - x
;EXITIF Z ; exact result
breq done ; optional faster code if already exact result (skip extra MUL and round-up)
IF NC ; result y too big
eor YL, YH ; undo current bit
ENDI
lsr YH ; next bit position
UNTIL C
IF !YL,0 ; LSB has been reset, therefore a new MUL is required
mul YL, YL ; result y^2 in PHI:PLO
sub PLO, RADLO ; subtracting needs same time as comparing, but simplifies rounding
sbc PHI, RADHI ; now PHI:PLO = y^2 - x
ENDI
; Up to here y = INT(SQRT(x)) is completed, but rounding is not yet correct,
; registers PHI:PLO hold the 2's complement of the remainder
; The 16 bit remainder of y = INT(SQRT(x)) is always in the range of 0 to 2*y,
; which means that almost 50% of the results are not correctly rounded.
; To do so, the result y should be rounded up if the remainder is > y.
; Just for x > 65280, y would then be 256, which is 9 bits, so 2 registers are required.
; The remainder of the rounded y then would be in the range -(y-1) to +(y).
; And the accuracy of the rounded y would be in the range -0,49... through +0,49...,
; which is approximately -+remainder/(2*y).
; Instead of calculating the true remainder and comparing against y,
; simply adding the 2's complement of the remainder and y is a few CPU cycles faster.
; Then rounding up must be done when the 16 bit sum of both is negative.
clr YH ; up to here there is no 9th bit
add PLO, YL
adc PHI, YH ; YH = 0 is helpful to add the carry
IF N ; the sum of y and the 2’s complement of the remainder is negative
adiw YH:YL, 1 ; round up = increment y (16 bit, so YH can become 1, otherwise YH stays 0)
ENDI
done:
ret
Nun muss ich zugeben, dass das nicht 100% strukturiert geschrieben ist, denn für kürzeste Rechenzeit wird die REPEAT-Schleife per BREQ direkt zum Ende verlassen, anstatt per EXITIF Z eine weitere Multiplikation und die Rundung zu durchlaufen.
Das ist eben der Vorteil der strukturierten Assembler-Programmierung, denn man programmiert immer noch maschinennah. An Übersichtlichkeit hat das aber nicht verloren, ganz im Gegenteil.
Ansonsten geht das Programm sehr sparsam (und trickreich) mit Registern um.
Falls man das wertvolle Y-Doppelregister anderweitig benötigt, kann man es durch zwei andere AVR-Register ersetzen, muss dann aber die Rundung geringfügig aufwendiger durchführen.
Vertrauen ist gut, Kontrolle ist besser
Damit mein s’AVR-Programm auch Hand und Fuß hat und die Rundungen alle exakt stimmen, habe ich es natürlich gründlich getestet, und zwar auf einem Arduino-UNO-Board mit einer 16-bit-REPEAT-Schleife für alle 2^16 Radikanden XH:XL von 0x0000 bis 0xFFFF.
Dieses Testprogramm gibt zeilenweise jeweils den Radikand und die zugehörige Quadratwurzel auf einem Terminal-Window aus, und zwar gleich per Tabulator getrennt, so dass man die Werte direkt in eine Excel-Tabelle[4] kopieren (Spalten wegen der HEX-Darstellung vorher als Text formatieren!) und mit eigenen Excel-Berechnungen vergleichen kann.
Bei allen Wurzelwerten wird korrekt gerundet, sprich die Genauigkeit liegt immer im Bereich -0,49... bis +0,49...
Ziemlich flott
Die per Scope gemessenen Rechenzeiten für die Quadratwurzeln liegen im Bereich von 1,12 µsec bis 6,87 µsec @16 MHz. Und das schaut als Hüllkurve auf dem Scope dann so aus:
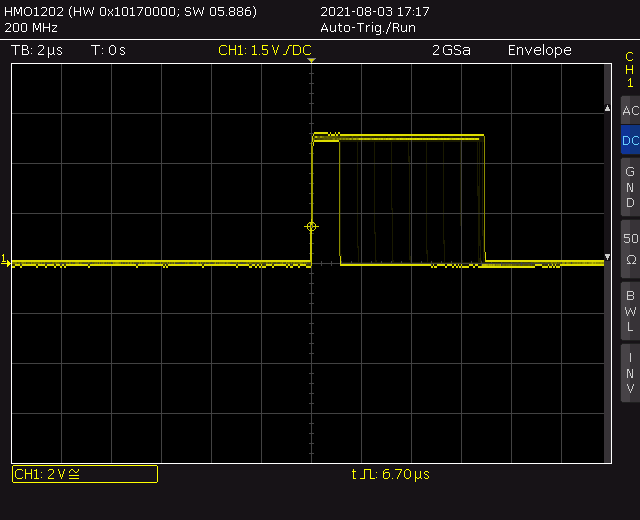
Die tatsächliche Rechenzeit ist 9 CPU-Zyklen weniger (1x I/O-Pin für das Scope + RCALL + RET).
"Netto" gerechnet sind es minimal 9 CPU-Zyklen (z. B. SQRT(16384)) bis maximal 2 + 7*11 + 10 + 12 = 101 CPU-Zyklen, also jeweils ohne RCALL- und RET-Befehl, aber korrekt gerundet.
Bei sehr genauem Hinschauen kann man auf dem Screenshot die 8 Bitstellen und ggf. die zusätzliche Multiplikation beim zurückgesetzten LSB erkennen, nämlich immer dann, wenn ein exaktes Ergebnis gefunden und per BREQ direkt ans Programmende gesprungen oder abschließend eine weitere Multiplikation für den richtigen Rest nötig wurde.
Da sich die Anzahl der verkürzten Zyklen aber in Grenzen hält, wird eine durchschnittliche Wurzel nach der beschriebenen Methode statt 101 kaum weniger, nämlich 97 CPU-Zyklen benötigen.
Beschleunigt
Nimmt man den BREQ heraus, werden zwar einige (wenige) Wurzelberechnungen etwas langsamer, aber es sind nur noch maximal 93 CPU-Zyklen bzw. ca. 5,8 µs @16 MHz (was etwa auch dem Durchschnitt bei allen 2^16 Quadratwurzeln entspricht).
Maximal 62 CPU-Zyklen, und noch weniger
Und wenn der Programmspeicher-Bedarf keine Rolle spielt, kann man die REPEAT-UNTIL-Schleife noch entrollen und dabei das Bit-Setzen/Rücksetzen nicht per Schieben und EOR, sondern direkt per SUBI erledigen. Dann können dafür allerdings nur "obere" AVR-Register verwendet werden.
Damit erreicht man dann weiter verkürzte Rechenzeiten, und zwar (wiederum ohne BREQ) maximal gerade einmal 62 AVR-CPU-Zyklen bzw. 3,875 µsec @16 MHz - wohlgemerkt mit sauber gerundetem Ergebnis und die Wurzel mit 9 Bit dargestellt.
Für dieses entrollte Programm sind allerdings 52 Worte (104 Byte) nötig (RET nicht mitgezählt).
Unter Berücksichtigung einiger Spezialfälle ließen sich beim entrollten Programm weitere Befehle einsparen und etwas Rechenzeit gewinnen, aber die Übersichtlichkeit verliert dabei.
Zum Beispiel solange die unteren 4 Bits des Ergebnisses alle 0 sind (sprich beim Abfragen der Bits 7 bis 4), muss man beim Vergleichen nur das High-Byte des Quadrats (bei mir PHI) berücksichtigen, was ich bei den maximal 62 CPU-Zyklen bereits gemacht habe.
Desweiteren könnte man wenigstens die oberen beiden Bits 7 und 6 einfach durch Abfragen des Radikanden-High-Bytes und durch geschicktes Setzen der Ergebnis-Bits ohne tatsächliche Multiplikation abhandeln (das Programm ist jetzt aber trotz strukturierter Programmierung nur noch mit reichlich Kommentaren zu verstehen) und dann wie gehabt mit Bit 5 weitermachen.
Mit dieser Methode bin ich bei maximal 56 AVR-CPU-Zyklen bzw. 3,5 µsec @16 MHz und 49 Programmspeicherworten angelangt (ohne RET), wiederum mit gerundetem Ergebnis und die Wurzel mit 9 Bit dargestellt.
Wenn korrektes Runden und der ganzzahlige Rest nicht interessieren, kann man 10 CPU-Zyklen und 8 Programmspeicherworte einsparen.
Kaum noch Scharm
Auch wenn das getunte Programm 1,8-fach schneller (und der Programmspeicherbedarf nur 1,4-fach größer) ist, hat es im Vergleich zur vorgestellten Schleife mit acht Durchläufen mächtig an Übersichtlichkeit und Scharm verloren.
Es hat mich nun doch noch interessiert, wie C-Programme das ganzzahlige Wurzelziehen nebst korrektem Runden für einen AVR-µC umsetzen.
Dazu habe ich mir ein kleines Arduino-Programm (C++) geschrieben und auf einem Arduino-UNO laufen lassen:
uint16_t radikand;
uint16_t wurzel;
Serial.println("Wurzel-Berechnung ...");
for (radikand = 0; radikand <= 65535; radikand++)
{
digitalWrite(LED_BUILTIN, HIGH);
wurzel = round(sqrt(radikand));
digitalWrite(LED_BUILTIN, LOW);
printf("%6u\t%3u\n", radikand, wurzel);
}
Überrascht war ich zunächst über den Speicherbedarf von 6.580 Byte für das Programm (wohl wegen der eingebundenen printf-Library) und zusätzlichen 222 Byte SRAM.
Die Rechenzeit pro Quadratwurzel beträgt typisch ca. 50 µsec bis knapp über 60 µsec @16 MHz. Im Schnitt liegt das beim Zehnfachen meiner obigen s’AVR-Programme!
Endlosschleife
Dann hat mich verblüfft, dass das Programm nach dem Abarbeiten der FOR-Schleife nicht wie vorgesehen stoppte, sondern die Schleife immer wieder von vorne begann.
Nun, das liegt daran, dass nach dem Inkrementieren von 65535 die 16-bit-Variable den Wert 0 annimmt und nicht 65536, was ein 17-Bit-Wert wäre.
Eine Compiler-Warnung gibt es bezüglich dieser gut versteckten Falle nicht.
Auch eine schlichte WHILE-Schleife endet bei demselben Endekriterium in derselben Endlosschleife.
Erst per DO-WHILE und einem anderen Endekriterium (nämlich dem 16-bit-Überlauf auf den Wert 0):
radikand = 0;
do
{
digitalWrite(LED_BUILTIN, HIGH);
wurzel = round(sqrt(radikand));
digitalWrite(LED_BUILTIN, LOW);
printf("%6u\t%3u\n", radikand, wurzel);
radikand++;
}
while(radikand != 0);
klappt die Schleife wie angedacht genau einmal über alle 2^16 möglichen Werte. Diese abschließende Abfrage erst nach dem Inkrementieren entspricht bei s’AVR einer REPEAT-UNTIL-Schleife.
Der Programmspeicherbedarf ist mit der DO-WHILE-Schleife sogar knapp weniger, nämlich 6.574 Byte und der SRAM-Bedarf beträgt wie zuvor 222 Byte.
GCC unter Atmel-Studio 7
GCC zeigt natürlich genau dasselbe Verhalten mit den genannten FOR- und WHILE-Schleifen. Aber per DO-WHILE klappt es auch bei GCC, sogar mit deutlich weniger Speicherbedarf, obwohl auch hier Routinen für printf eingebunden sind:
Program Memory Usage: 2678 bytes 8,2 % Full
Data Memory Usage: 70 bytes 3,4 % Full
Im Vergleich zu C++ sind die Rechenzeiten deutlich kürzer. Sie liegen im Bereich von 40 µsec bis 50 µsec @16 MHz.
Die Unterschiede im Code zwischen C++ und GCC habe ich nicht weiter analysiert. Lediglich zwei GCC-Unterprogramme habe ich näher angeschaut:
Die Routine "sqrt" arbeitet überraschenderweise komplett ohne MUL-Befehle (bei beiden C-Compilern) und benötigt bei GCC dafür 252 Byte zzgl. zwei aufgerufenen Unterprogrammen à 100 Byte und 24 Byte.
Und die Routine "round" benötigt weitere 160 Byte, also zusammen 536 Byte. Kein Wunder, dass die Rechenzeiten gegenüber s’AVR so viel größer sind.
Summierende Wurzel-Approximation (23.8.2021)
Die doch relativ langsame Quadratwurzel-Berechnung per GCC und C++ hat mich dazu inspiriert, einen weiteren Lösungsansatz vorzustellen, der im Mittel nicht viel langsamer ist, aber ausgesprochen wenig Resourcen benötigt und dabei ganz auf Multiplikationen verzichtet (weder per Hardware, noch per Software).
Dieser Algorithmus - ich will ihn summierende Wurzel-Approximation nennen - bestimmt die Quadratwurzel aus einem gegebenen Radikanden, in dem die gesuchte Wurzel (die Radix) beginnend mit 0 durch Inkrementieren gesucht und gefunden wird, und zwar auf Anhieb mit korrekter Rundung.
Nun, das könnte man zunächst einfach durch Quadrieren der Radix (zwangsläufig eine Multiplikation, die vermieden werden sollte) und Vergleichen mit dem Radikanden finden, dann allerdings noch ohne die korrekte Rundung.
Es gibt aber auch einen ganz anderen Weg, der mir beiläufig in den Sinn gekommen ist, als ich nach einer schnellen (Auf-) Rundungsmethode für meine obige s’AVR-basierende Wurzelberechnung gesucht habe.
Hierzu habe ich in einer Tabelle die Schwellen markiert, bei welchen das Aufrunden nötig wird. Und dabei ist mir aufgefallen, dass die Anzahl gleicher Wurzelwerte bzw. der Abstand der Rundungsschwellen gemäß einer arithmetischen Reihe 2. Ordnung ansteigt, nämlich:
1, 3, 7, 13, ..., 64771, 65281
Nun könnte man die einzelnen Glieder dieser Reihe zwar aufwendig per Formel berechnen, was aber überflüssig ist, wenn man die Abstände der einzelnen Glieder dieser arithmetischen Reihe[6] betrachtet, nämlich:
2, 4, 6, 8, ... 508, 510
Das sind also lauter stetig ansteigende gerade Zahlen.
Mit dieser Erkenntnis kann für die "Wurzelfindung" die Berechnung der Rundungsschwellen während dem Inkrementieren der Radix einfach durch Akkumulieren von geraden Zahlen (nämlich dem Doppelten der laufenden Radix) geschehen, beginnend mit dem Startwert 1.
Anhand dieser Reihe mit insgesamt 257 Gliedern kann man schließlich die gesuchte und korrekt gerundete Radix 0...256 finden, indem man den gegebenen Radikanden mit den akkumulierten Schwellenwerten (beginnend mit 1) vergleicht.
Das waren jetzt viele Worte für ein ausgesprochen einfaches s’AVR-Programm:
; Square root by adding up and comparing with radicand, (c) 23-AUG-2021 Eberhard Haug
SQRT16au: ; find yh:yl = rounded integer SQRT(xh:xl)
clr cnth
clr cntl ; clear even number counter
clr acch
ldi accl, 1 ; set limit accumulator to 0x0001
movw yh:yl, cnth:cntl ; clr result counter
LOOP ; even number cnth:cntl = 0, 2, 4, 6, ...
; limit accumulator acch:accl = 1, 3, 7, 13, ...
cp xl, accl ; xl
cpc xh, acch ; xh
EXITIF C ; radicand below limit acch:accl, correctly rounded radix found
adiw yh:yl, 1 ; next y
adiw cnth:cntl, 2 ; next even number 2, 4, 6, 8, ...
add accl, cntl ; next limit 3, 7, 13, ...
adc acch, cnth
EXITIF C ; last step if x > 65.280 (+512 = 65.782)
; final radix = 0x100 (256)
ENDL
ret
Das sind gerade einmal 14 Assembler-Befehle (28 Bytes) für das ganze Programm (ohne RET), wiederum mit dem Hinweis, dass das Ergebnis für die Quadratwurzel 9 Bit genau und korrekt gerundet ist.
Dieses Programm benötigt keine Multiplikationen, sondern ausschließlich Additionen und Vergleiche. Zusätzlich zum Radikanden im Doppelregister XH:XL, werden nur 6 weitere AVR-Register (4 davon sind zwei Doppelregister) verwendet (die bei Bedarf gerettet werden müssen).
Im Vergleich zum ursprünglichen Lösungsansatz mit sukzessiver Approximation (benötigt 36 Byte Programmspeicher und insgesamt nur 6 AVR-Register) ist jenes mit summierender Approximation jedoch deutlich langsamer, nämlich von ca. 1 µsec bis ca. 193 µsec mit dem Radikanden linear ansteigend, sprich im Mittel ca. 86 µsec @16 MHz.
Damit ist es im Mittel etwa halb so schnell wie die C++/GCC-Programme.
Aber es ist ein sehr einfaches und übersichtliches s’AVR-Programm mit sehr wenigen Lines-of-Code.
Man könnte beinahe in Versuchung geraten, nach diesem Prinzip einen "Wurzelzieher" per Standard-CMOS-Logik aufzubauen.
Subtrahierende Wurzel-Approximation (8.3.2023)
Nachdem ich mir kürzlich das Ziehen der Quadratwurzel auf mechanischen Rechenmaschinen näher angeschaut hatte, fiel mir mein aufaddierender Wurzelzieher wieder ein, bei dem man den Spieß auch umdrehen kann, um die Quadratwurzel zu finden.
Und genau diese Methode hat August Toepler (1836 - 1912) für mechanische Rechenmaschinen angewandt, indem er vom Radikanden solange die ungeraden Zahlen[6] 1, 3, 5, 7 ... abgezogen[7] hat, bis die Überlauf- bzw. Behalte-Glocke geschlagen hat. Das ist bei einer mechanischen Maschine natürlich deutlich einfacher als akkumulierte Werte zu vergleichen.
Der Toepler-Algorithmus hat jedoch ein kleines Manko, denn das Ergebnis ist (insbesondere bei der Integer-Berechnung) nicht korrekt gerundet.
Einfache Abhilfe schafft aber eine kleine Änderung: Man subtrahiert anfangs zwar ebenfalls die 1, macht dann aber bei Bedarf mit den geraden Zahlen 2, 4, 6, ... weiter, wiederum bis ein negativer Wert entsteht.
Dieser modifizierte Toepler-Algorithmus per s’AVR-Programm umgesetzt, schaut dann so aus:
; Square root by subtracting away from radicand, (c) 8-MAR-2023 Eberhard Haug
; First always check for radicant = 0 by subtracting 1,
; and then for all other radicands subtract even nummbers 2, 4, ...
; XH:XL = radicand (changed afterwards!), YH:YL = SQRT(XH:XL),
; CNTH:CNTL = even number counter = (1), 2, 4, 6 ...
SQRT16sa: ; find YH:YL = rounded SQRT(XH:XL)
; using 3 double registers within R24 through R31
clr YH
clr YL ; clear result register
sbiw XH:XL, 1 ; X := X - 1, initially subtract 1 (for all radicands!)
IF C ; radicand 0 requires separate handling to keep LOOP short
ret ; Y := 0
ENDI
ldi YL, 1 ; Y := 1
clr CNTH
ldi CNTL, 2 ; set even number counter to 0x0002 (instead of 3)
LOOP
sub XL, CNTL ; X := X - CNT
sbc XH, CNTH
EXITIF C ; radicand now is negative, correctly rounded radix found
adiw YH:YL, 1 ; next Y
adiw CNTH:CNTL, 2 ; next even number 4, 6, 8, ...
ENDL
ret
Dieser Algorithmus lässt sich leider nicht (wie bei der addierenden Methode) mit möglichst wenig Befehlen vollständig innerhalb der Schleife umsetzen, da 1, 2, 4, 6, 8 ... keine arithmetische Reihe ist.
Er ist aber dennoch einiges schneller als der addierende Algorithmus, siehe Screenshot mit der schnellsten und der langsamsten Berechnung:
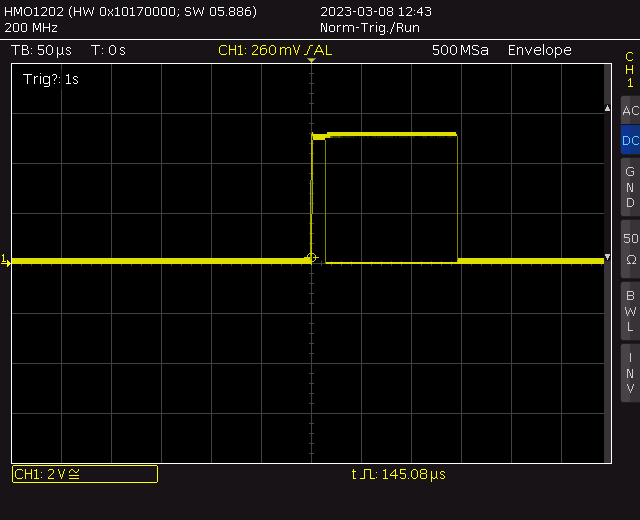
Die tatsächliche Rechenzeit ist auch hier wiederum 9 CPU-Zyklen weniger als angezeigt (1x I/O-Pin für das Scope + RCALL + RET), sprich jetzt nur noch rund 140 µsec @16 MHz für SQRT(0xffff) = 0x100 und kommt somit im Mittel den speicherfressenden C++/GCC-Programmen per sukzessiver Approximation schon sehr nahe.
Das s’AVR-Programm benötigt jetzt nur noch 12 Assembler-Befehle (ohne RET) und geht mit insgesamt drei Doppelregistern (einschließlich Radikand) auch etwas sparsamer mit den AVR-Registern um.
Und man könnte nun noch mehr in Versuchung geraten, nach dem subtrahierenden Prinzip einen "Wurzelzieher" per Standard-CMOS-Logik aufzubauen ...
Noch ein wenig sparsamer und schneller (22.3.2023)
Mit der Erkenntnis bezüglich dem versteckten Ergebnis beim 4-bit-Rechenwerk kann man das Doppelregister YH:YL einsparen bzw. als Ersatz für den Zähler CNTH:CNTL nehmen, so dass man insgesamt nur noch zwei Doppelregister benötigt und das Programm sogar noch um einiges schneller wird (weniger als maximal 113 µs @16 MHz), wobei die Anzahl der AVR-Assembler-Befehle dabei dieselbe ist.
; 22-MAR-2023 Improved Toepler version using only 2 AVR double registers
; XH:XL = radicand (changed afterwards!), CNTH:CNTL = SQRT(XH:XL),
; CNTH:CNTL = initially even number counter = (1), 2, 4, 6 ...
SQRT16TM: ; find CNTH:CNTL = rounded SQRT(XH:XL)
; using 2 double registers within R24 through R31
clr CNTH
clr CNTL ; clear result register
sbiw XH:XL, 1 ; X := X - 1, initially subtract 1 (for all radicands!)
IF C ; radicand 0 requires separate handling ahead to keep LOOP short
ret ; CNT := 0
ENDI
ldi CNTL, 2 ; set even number counter to 0x0002 (instead of 3) = rounded Toepler
LOOP
sub XL, CNTL ; X := X - CNT
sbc XH, CNTH
EXITIF C ; radicand now is negative, correctly rounded radix found
adiw CNTH:CNTL, 2 ; next even number 4, 6, 8, ...
ENDL
; until here CNTH:CNTL is twice the correctly rounded result
lsr CNTH ; divide by 2
ror CNTL
ret ; CNTH:CNTL = rounded SQRT(XH:XL)
Die gerundete Quadratwurzel ist einfach die Hälfte des Zählers nach Verlassen der Schleife.
Richtig schnell wird es dann mit dem Turbo-Toepler, nämlich maximal 15 µs @16 MHz.
Das Toepler-Verfahren auf einem 4-bit-Rechenwerk (20.3.2023)
Zwar ist es kein CMOS-Rechenwerk, das einen 16-bit-Wert oder gar einen 32-bit-Wert radiziert (und natürlich auch das Ergebnis anzeigt), dafür ist es ein handbedientes 4-bit-Rechenwerk bestehend aus vier Volladdierern, realisiert auf einem Steckbrett mit Modulen in historischer Germanium-Technologie aus den 1960-er Jahren[10]:

Diese Module der B8-Serie sind einfache digitale Schaltungen, realisiert mit diskreten Germanium-Transistoren und -Dioden, Widerständen und Kondensatoren, vergossen in Kunststoffgehäusen unterschiedlicher Farbe.
Sie sind quasi die Vorläufer monolithisch integrierter Schaltkreise und wurden u. a. von Valvo unter der Bezeichnung Combi-Elemente angeboten. Bei Philips hießen genau dieselben Schaltkreise Digital Circuit Blocks Series-1. Sie wurden für Taktraten von bis zu 100 kHz spezifiziert.
Der Aufwand, mit diesen spartanischen Modulen ein einfaches Rechenwerk zu realisieren, ist entsprechend groß.
Angeregt durch das Advents-Projekt 2022 des Computermuseums der Universität Stuttgart habe ich mich dennoch dazu hinreißen lassen, mit diesen Combi-Elementen ein 4-Bit-Rechenwerk auf einem größeren Steckbrett aufzubauen. Mehr dazu auf der Website des Computermuseums bzw. dessen YouTube-Kanal.
Die Quadratwurzel von Hand gezogen
Mit diesem Rechenwerk kann man wie mit einer mechanischen Rechenmaschine tatsächlich auch eine Quadratwurzel ziehen, wenn auch nur von einem 4-bit-Radikanden.
Da es kein separates Umdrehungszählwerk gibt, muss man die Anzahl der Subtraktionen an den Fingern mitzählen.
Aber eine Hand reicht ja dafür, die andere stellt die Schalter und subtrahiert. :-)
Damit es einigermaßen realistisch wird, muss die Glocke schlagen, wenn bei einer Subtraktion ein negativer Wert, sprich ein Behalte auftritt. Das ist bei der Toepler-Methode der Hinweis, dass man einmal zu viel abgezogen hat.
Dann wird bei der mechanischen Rechenmaschine die letzte Subtraktion durch eine Addition des letzten Subtrahenden rückgängig gemacht und in der nächsten 10-er- oder 100-er-Gruppe (je nach bevorzugter Methode) weiter geschoben und gekurbelt.
Bei meinem binären Rechenwerk ist die Glocke der Hinweis, dass man nicht mehr weiterzählt und somit das Ergebnis vorliegt, quasi auf der Hand.
Carry und Borrow, Übertrag und Behalte
Normalerweise unterstützen binäre Rechenwerke (wie die inzwischen historische ALU 74’181 und ähnliche) nur den Additions-Übertrag, das Carry.
Selbst einige (wenige) µProzessoren und µController (z. B. 6502, PIC, SX28-Familie) haben auch nur ein solches Übertrags-Carry, das genauso bei Subtraktionen verwendet wird, die als Addition von Zweierkomplementen durchgeführt werden. In diesen Fällen muss das Carry bei Subtraktionen invertiert betrachtet werden und nicht als Behalte.
Die meisten anderen µProzessoren und µController (so auch die AVR-µC) unterstützen dagegen neben dem Additions-Übertrag ein echtes Subtraktions-Behalte, das Borrow, das im Statusregister zwar ebenfalls als Carry aufgeführt ist, aber bei Subtraktionen wie gewohnt als Behalte interpretiert wird (siehe auch hier und alle meine s’AVR-Beispiele).
Die Behalte-Glocke
Damit die Rechenwerk-Glocke bei einem Behalte schlägt (bzw. bei einem negativen Ergebnis, wie bei einer mechanischen Rechenmaschine), habe ich bei meinem 4-bit-Rechenwerk einfach das Trigger-Signal für die Glocke mit zwei weiteren Combi-Elementen invertiert[9], wenn am Bedien-Panel auf Subtraktion umgeschaltet ist:

Das (modifizierte) Toepler-Verfahren demonstriert
Mit einer Behalte-Glocke kann das Quadratwurzelziehen per 4-bit-Rechenwerk mehr oder weniger wie bei einer mechanischen Rechenmaschine erfolgen.
Das "Programm" (natürlich strukturiert geschrieben) für die korrekt gerundete Quadratwurzel würde dann wie folgt ausschauen:
SQRT4_gerundet: ; Quadratwurzel eines 4-bit-Radikanden auf dem 4-bit-Rechenwerk
lade den Akkumulator mit dem Radikanden
stelle das Rechenwerk auf Subtraktion
stelle den Fingerzähler auf 0
stelle die Eingabe auf den Wert 1 ; das Zweierkomplement wird angezeigt
subtrahiere den eingestellten Wert mit der Sigma-Taste
FALLS Behalte-Glocke schlägt
beende die Berechnung ; das Ergebnis ist null
FALLSENDE
stelle den Fingerzähler auf 1
stelle die Eingabe auf den Wert 2 ; bzw. 3 für das nicht gerundete Verfahren
SCHLEIFE
subtrahiere den eingestellten Wert mit der Sigma-Taste
FALLS Behalte-Glocke schlägt
beende die Berechnung ; der Fingerzähler ist die gerundete Quadratwurzel
FALLSENDE
erhöhe den Fingerzähler um 1
erhöhe die Eingabe um 2
SCHLEIFEENDE ; zurück zum Schleifenanfang
; das Ergebnis der gerundeten Quadratwurzel wird durch den Fingerzähler angezeigt
Das schaut komplizierter aus, als es tatsächlich ist.
Hier der Rechenvorgang für den Radikanden 15 als kleine Tabelle dargestellt:
Das Ergebnis steht auch versteckt in der Eingabe
Falls das mit dem Fingerzähler (meistens) nicht zuverlässig klappt, kann man nach dem Berechnen der gerundeten Quadratwurzel einfach den Schalter von Subtraktion auf Addition umschalten und erhält bei den Eingabe-Schaltern das Doppelte der Quadratwurzel per LEDs angezeigt - eine Eigenschaft des Toepler-Verfahrens.
Wegen den kleinen Radikanden von 0 bis 15 werden per Eingabe nur die Werte 1, 2, 4, 6 und 8 abgezogen (linke Spalte in der Tabelle) bis die Behalte-Glocke schlägt. Bis auf den ersten Wert sind es lauter gerade Zahlen, so dass das Halbieren bis auf das Ergebnis beim Radikanden 0 immer eindeutig funktioniert.
Beim digitalen Halbieren durch Rechtsschieben der Eingabeanzeige würde die einsame Eins (die für das Verfahren zwingend notwendig ist) in der letzten Stelle sogar verschwinden, so dass man immer direkt das richtige Ergebnis erhalten würde, ganz ohne Mitzählen.
Da beim einfachen 4-bit-Rechenwerk keine Schiebeoperationen vorgesehen sind, muss das in Gedanken geschehen.
Fazit
Das heißt, man deckt nach dem Wurzelziehen (Behalte-Glocke hat geschlagen!) und Umschalten auf Addition einfach die 1-er-Stelle des Subtrahenden (= Eingabe-LEDs) ab und schon bekommt man die korrekt gerundete Quadratwurzel mit den drei linken LEDs (8-4-2) angezeigt, die man mit der Wertigkeit 4-2-1 interpretiert und so die Zahlenwerte 0, 1, 2, 3 oder 4 als Radix der Radikanden 0 bis 15 erhält
Hier das Ergebnis beim Radizieren von 15 nach dem Umschalten der Eingabe auf Addition:

Die letzte Subtraktion von 8 (laut unterer Beschriftung) hat im Akkumulator -6 (= 2-er-Komplement der angezeigten 10) ergeben, siehe auch Tabelle.
CY = 0 heißt (bei meinem derzeitigen Rechenwerk) Behalte = 1 --> Glocke wurde getriggert.
Die richtig gerundete Quadratwurzel von 15 ist laut mittlerer Beschriftung also 4.
Das Video
Bei Gelegenheit werde ich ein Video nachreichen, das sowohl das Original-Toepler-Verfahren mit der Subtrahenden-Folge 1-3-5-7 (liefert die Ganzzahl der Quadratwurzel) als auch die von mir vorgeschlagene Variante mit der Subtrahenden-Folge 1-2-4-6-8 für die korrekt gerundete Quadratwurzel (wie im "Programm") jeweils für alle Radikanden 0 bis 15 demonstriert.
Die Turbo-Toepler-Wurzel (15.3.2023)
Die obige subtrahierende Wurzel-Approximation wird in einem Durchgang über die volle 16-bit-Breite des Radikanden durchgeführt und benötigt deshalb entsprechend viele Schleifendurchgänge.
Nachfolgend wird eine beschleunigte Methode beschrieben, wie sie im Prinzip auch bei mechanischen Rechenmaschinen angewandt wird, bei denen man sich für eine größere Genauigkeit der Wurzel sonst die Finger wund schieben und kurbeln würde.
Dort wird der Radikand in 100-er Gruppen aufgeteilt und deren 10er-Stellen a und b werden einzeln per Toepler-Verfahren und Anwendung der ersten binomischen Formel radiziert. Jede 100er-Gruppe des Radikanden lässt sich dann so darstellen:
(10a+b)2 = 100a2 + 2*10ab + b2
Wie das (immer noch zeitaufwendige) Radizieren damit bei mechanischen Rechenmaschinen genau funktioniert, findet man zuhauf im WWW beschrieben.
Ran an die Nibbles
Sinngemäß kann man zum Berechnen einer 16-Bit-Quadratwurzel die 8-bit-Radix in zwei Nibbles a und b aufteilen und dann gilt für den 16-bit-Radikanden:
(16a+b)2 = 256a2 + 2*16ab + b2
Zum Berechnen der Quadratwurzel (also 16a+b) betrachtet man zunächst das High-Byte des Radikanden gemäß oben beschriebenem Toepler-Verfahren, jedoch mit der ursprünglichen arithmetischen Reihe a2 = 1 + 3 + 5 + ... + (2a-1), die keine Rundung durchführt.
Das Ergebnis ist dann das High-Nibble a (mit der Wertigkeit 16*a) der Radix, und der Anteil 256a2 des Radikanden ist damit abgearbeitet, womit noch ein Rest 2*16ab + b2 übrig bleibt.
Ab hier ein wenig komplizierter
Vom Rest des Radikanden werden schließlich genau so lange die linear ansteigenden Werte 2*(16a)+1, 2*(16a)+3, 2*(16a)+5, ... abgezogen und die Anzahl der Subtraktionen b ab null hochgezählt, bis das Ergebnis der Subtraktion negativ[8] wird.
Genau dann ist b das gesuchte Low-Nibble der (noch nicht gerundeten) Quadratwurzel.
Da sowohl a als auch b nur 4 Bit breit sind, können beide auch nur Werte 0...15 annehmen. Das heißt, die Anzahl der Durchläufe für die beiden Subtraktionsschleifen hält sich in Grenzen, wodurch die Berechnungszeit für die Quadratwurzel deutlich kürzer wird.
Turbo-Toepler programmiert
Als strukturiertes s’AVR-Programm, das wiederum ganz ohne Hardware-Multiplikation auskommt (also ggf. ohne Abstriche auch auf älteren ATtinys läuft), schaut das dann so aus:
; 16-bit Square Root SQRT16tt - the Turbo Toepler Version, 15-MAR-2023 (c) Eberhard Haug
; XH:XL = radicand (changed afterwards!), YH:YL = SQRT(XH:XL),
; CNTH:CNTL is the series counter, also handling 2x the high nibble of the result
; Series 1, 3, 5, 7 ... generates INT(SQRT(Y)), last delta -1...-511.
; An optional very simple rounding up is included.
SQRT16tt: ; find YH:YL = SQRT(XH:XL)
; using 3 double AVR registers within R24 through R31
; initially handle high byte XH
clr YL ; clear result register (low byte is sufficient)
ldi CNTH, 1 ; for high byte start series subtracting 1 etc. from high byte
LOOP
sub XH, CNTH ; X := X - odd numbers 1, 3, 5 ...
EXITIF C ; radicand now is negative, high byte radix found
subi YL, -16 ; Y := Y + 16, increment upper nibble of YL
subi CNTH, -2 ; next odd number 3, 5, 7, ...
ENDL
add XH, CNTH ; XH := XH + CNTH, re-do last subtraction as result was negative
; for low byte XL take care of binomial formula: (16*a + b)^2 = 256*a^2 + 2*16*a*b + b^2,
; so besides the series 1, 3, 5, 7 also 32*(high nibble of YL) must be subtracted,
; which means that CNT := 32*(high nibble of YL) + series 1, 3, 5, ...
; up to here the low nibble of YL still is 0b0000
clr CNTH
mov CNTL, YL ; take a copy of YL, the result of the high byte
lsl CNTL ; 2 * YL = 2 * 16 * high nibble of YL
rol CNTH ; now a 16 bit register is required
subi CNTL, -1 ; in addition prepare CNT for series 1, 3, 5, ...,
LOOP
sub XL, CNTL ; X := X - (2*16a + series 1, 3, 5 ...)
sbc XH, CNTH
EXITIF C ; radicand now is negative, integer of radix found
subi YL, -1 ; Y := Y + 1, next Y, only lower nibble should be affected
adiw CNTH:CNTL, 2 ; next odd number 3, 5, 7, ...
ENDL
; rounding up, if wanted
; up to here there is no 9th result bit, the result is YL = int(sqrt(x))
clr YH ; YH = 0 is helpful to add the carry
add XL, YL
adc XH, YH ; a carry should be generated if X + Y ≥ 0
; IF C ; absolute value of remainder XH:XL is ≤ result YH:YL
; adiw YH:YL, 1 ; round up = increment YH:YL, now also YH can become 1
; ENDI
; instead of IF-ENDI a slightly faster code directly using the carry:
adc YL, YH ; add carry if any (still YH = 0)
adc YH, YH ; now rounded 9-bit result YH:YL
ret
Schnell und trickreich gerundet
Wie bei obigem s’AVR-Programm SQRT16 (sukzessive Approximation) wird auch hier bei Bedarf mit einer einfachen 16-bit-Addition korrekt (auf-) gerundet. Dabei wird das entstehende Carry trickreich ohne weitere Abfrage direkt zum Inkrementieren des Ergebnisses verwendet.
Die mathematische Erklärung (18.3.2023)
Natürlich habe ich alle 2^16 Quadratwurzeln auf ein richtig gerundetes Ergebnis überprüft. Dennoch sei eine mathematische Erklärung der trickreichen Rundung nachgereicht.
Nach Beenden der zweiten Schleife steht der Rest der letzten Subtraktion als negativer Wert (Zweierkomplement) in XH:XL und das Carry ist wegen der Subtraktion als Unterlauf (= Borrow) gesetzt = Abfrage für Ergebnis gefunden.
Der in XH:XL stehende Rest liegt je nach Radikand im Bereich -1 bis -511.
Wenn der Betrag des Rests größer ist als die Radix, wurde automatisch korrekt abgerundet.
Ist der Betrag des Rests aber kleiner oder gleich der Radix, muss das Ergebnis aufgerundet werden:
|XH:XL| ≤ YH:YL
alles auf eine Seite:
0 ≤ YH:YL - |XH:XL|
Statt der Subtraktion des Betrags kann man aber auch gleich das bereits vorhandene Zweierkomplement addieren:
0 ≤ YH:YL + XH:XL
Mit dieser Überlegung hätte man nach der Addition an dieser Stelle wie folgt abfragen können:
IF NOT N ; the sum of remainder XH:XL (negative) and result YH:YL is positive
adiw YH:YL, 1 ; round up = increment YH:YL
ENDI
Einerseits ist die Summe aus einem negativen Rest und dem Ergebnis beim Aufrunden positiv. Aber durch die Addition des negativen Werts erfolgt dann auch ein Überlauf und das Carry wird gesetzt, das man entweder ebenfalls abfragen könnte (siehe auskommentierte Befehle) oder aber ohne weitere Abfrage ganz praktisch zum Inkrementieren einfach durch Addition des Übertrags weiterverwendet.
Ziemlich flott und dennoch sparsam
Zwar ist der Befehlsaufwand mit 24 AVR-Assembler-Befehlen (einschließlich Rundung) nun fast doppelt so groß wie bei der subtrahierenden Wurzel-Approximation, dafür wird die Quadratwurzel aber 10x schneller berechnet (maximal 15 µs @16 MHz) und ist somit ca. 4x bzw. 3x schneller als die (normalerweise sehr schnelle) sukzessive Approximation per C++ bzw. GCC.
Im Vergleich zur sukzessiven Approximation per s’AVR ist sie aber immer noch rund 4x langsamer, benötigt aber auch nur die Hälfte der AVR-Assembler-Befehle und kommt ganz ohne Hardware-Multiplikation aus.
Größere Radikanden
Zur Berechnung der Quadratwurzel größerer Radikanden (24 Bit, 32 Bit etc.) kann man die beschriebene Methode durch byte-weises Radizieren anwenden, so wie das bei mechanischen Rechenmaschinen sinngemäß im Dezimalsystem gemacht wird.
Die eher nicht so häufig benötigte dritte Wurzel aus einer Zahl (die Kubikwurzel) lässt sich sinngemäß mit den oben beschriebenen Verfahren berechnen.
Zunächst muss man jedoch klären, wie groß der Radikand sein darf.
Für ein 8-bit-Ergebnis bieten sich 24 Bit als Radikand an. Dann wird der Aufwand für die Berechnung doch einiges größer.
Falls es aber bei 16 Bit bleiben soll, ist das Ergebnis maximal 40. Dann wird es besonders bei der sukzessiven Approximation sehr einfach, denn statt der Quadratbildung muss man nur ein weiteres mal multiplizieren und man beginnt beim Bit-Setzen eben bei Bit 5 statt bei Bit 7.
Bei der inkrementalen Approximation muss man doch erst einmal etwas genauer hinschauen, denn Kubikzahlen werden durch die Summe einer arithmetische Reihe 3. Ordnung gebildet:
1, 8, 27, 64, 125, 216, ...
Das bedeutet, dass man im Unterschied zur Quadratwurzel eine weitere Akkumulation benötigt.
Die 2. Differenzreihe schaut wie folgt aus:
12, 18, 24, 30, ...
Die zum Akkumulieren ebenfalls interessierende 3. Differenzreihe ist zwar konstant (bei den Quadratzahlen ist es die 2. Differenzreihe mit der konstanten Differenz 2):
6, 6, 6, ...
Aber leider sind die für die Rundungsschwellen nötigen Differenzen nicht immer dieselben (wie bei der Quadratwurzel) sondern etwas holprig, nämlich:
6, 7, 4, 7, 6, 7, 4, 7, ... (Mittelwert 6)
Das lässt sich wegen der Periodizität sicher auch programmiertechnisch umsetzen, schneller wird es jedoch durch entrollen, also viermal hintereinander mit den verschiedenen Differenzen 6, 7, 4 und 7 akkumulieren etc. und den Radikanden auf die so erzeugten Rundungsschwellen
1, 4, 16, 43, 92, 167 ...
für die gesuchte und korrekt gerundete Kubikwurzel abfragen.
Falls der Radikand nur 16 Bit groß ist, reichen für den "Even Counter" obigen Programms (der hier aber statt 2 abwechselnd 6, 7, 4 und 7 aufaddiert) auch 8 Bit, denn das 41. Glied der 2. Differenzreihe hat den Wert 252 und ist wegen dem größeren Startwert von 12 größer als der größte Wert dieses "Even Counters". Register YH wird nicht benötigt, da die gesuchte Kubikwurzel bei einem 16-bit-Radikanden maximal 40 ist.
[1] s’AVR führt nur 8-bit-Vergleiche und diese generell ohne Vorzeichen aus, siehe Handbuch.
[2] Ivan Flores: "The logic of Computer Arithmetic".
[3] Der MK68200 hat eine ähnliche Architektur wie der 68000, aber nur 16 Bit breite Register (8 Datenregister, 6 Adressregister, PC, Stackpointer und Statusregister).
Allerdings hat er noch 128x16 SRAM, 2Kx16 ROM, gemultiplexten externen 16-bit-Adress/Daten-Bus, 3x 16-bit-Timer, eine serielle Schnittstelle (USART), Parallel-I/O-Ports (16/8 Bit), einen Interrupt-Controller und einen Quarzoszillator dazu bekommen. Der MK68200 ist also ein echter Single-Chip-µC.
Der Befehlssatz ist für Embedded-Applikationen ausgelegt (einschließlich MULU/MULS, DIV, BCD-Arithmetik, umfangreiche Bit-Manipulation und u. a. außer NEG auch ein NEGC für ein schnelles 2er-Komplement über mehrere Worte). Die meisten Befehle zur Datenmanipulation können wahlweise für 8 oder 16 Bit Datenbreite ausgeführt werden.
Allerdings sind die Ausführungszeiten wie bei jeder CISC-CPU deutlich länger als z. B. bei den AVR-RISC-CPUs. So benötigen alle "einfachen" Befehle (ADD, MOV ...) meist 3 CPU-Zyklen und z. B. eine 16x16-Multiplikation bereits 21 CPU-Zyklen. Der CPU-Takt der ersten Generation betrug 4 MHz oder 6 MHz (mit einem 8MHz-Quarz bzw. 12MHz-Quarz).
Es gab zwei Chip-Versionen MK68201 und MK68211 im 48-Pin-DIP mit unterschiedlichen Bus-Steuersignalen, nämlich UPC (68000-kompatible Signale) und GP (General Purpose) für Master/Slave-Anwendungen. Per MODE und einem weiteren Pin konnte man während Reset zwischen internem Programmspeicher (ROM) und jeweiligem externem Bus mit unterschiedlichem Speicher-Mapping umschalten.
Kundenspezifische ROM-Ausführungen erhielten die Bezeichnung MK41xxx (MK68201) bzw. MK42xxx (MK68211).
In einem 84-Pin-LCC gab es die entsprechenden Emulator-Chips als MK68E201/MK68E211, die den internen Adress/Datenbus und die zugehörigen Steuersignale an separaten Pins herausgeführt hatten. Diese Chips wurden auch auf Evalboards eingesetzt.
Falls jemand ein MK68200-Evalboard "übrig" hat: Ich hätte Interesse daran. Das Handbuch habe ich noch.
Hier ein Chip-Foto des MK68200 aus meiner Sammlung:

Rechts oben erkennt man eine Markierung UTC MOSTEK MK68200 RAINBOW ©1982.
[4] Bis einschließlich Excel 2006 lassen sich bis zu 2^16 Tabellen-Zeilen bearbeiten. Das ist also gerade noch für den SQRT16-Test ausreichend, aber für eine Kopfzeile (ggf. mit Filter) reicht es nicht mehr. :-(
[5] Zu allem Überfluss beginnen alle weiteren FOR-Schleifen mit 0, selbst wenn der ursprüngliche Startwert ungleich 0 ist.
[6] Bekanntermaßen gilt für das Quadrat diese Summenformel: 1 + 3 + 5 + 7 + ... + (2*x - 1) = x2
Interessant ist, dass die Reihe der Differenzschritte der Rundungsschwellen der Summenformel für die Quadratbildung sehr ähnlich sind, nämlich:
2 + 4 + 6 + ... + (2*x-2) + 2*x = 1+1 + 3+1 + 5+1 + 7+1 + ... + 2*x = x*(x+1) = x2 + x
Diese Formel bestätigt auch obige Feststellung im ersten s’AVR-Quellprogramm, dass der Rest bis zum Zweifachen von INT(SQRT(x)) betragen kann (letztes Glied der Reihe), also z. B. 65535 - 2552 = 510 = 2*256.
[7] Wegen der Berechnung im Dezimalsystem wird immer in 100-er Gruppen gerechnet und deshalb zusätzlich per erster binomischer Formel korrigiert.
[8] Bei mechanischen Rechenmaschinen erklingt dann meist die Glocke.
[9] Mangels freien Steuerleitungen zum Rechenwerk-Steckbrett erfolgt die Invertierung auf dem Glocken-Steckbrett. Deshalb zeigt die CY-LED immer noch den Additions-Übertrag an.
[10] Bestimmt war der "Computer Nr. 3", den France Gall 1968 besungen hat, auch mit solchen Modulen aufgebaut. :-)